题目内容
4.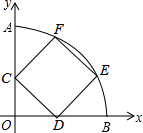 如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )
如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )| A. | 3 | B. | $\frac{5(\sqrt{5}-1)}{2}$ | C. | $\sqrt{10}$ | D. | 以上都不正确 |
分析 过O作OG⊥EF,交CD于点H,连接OF,设CH=a,根据正方形的性质和等腰直角三角形的性质可得OG=3a,在Rt△OEG中,根据勾股定理可得a的值,进一步得到正方形CDEF的边长.
解答 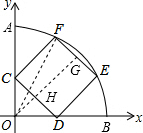 解:过O作OG⊥EF,交CD于点H,连接OF,
解:过O作OG⊥EF,交CD于点H,连接OF,
设CH=a,
∵四边形CDEF是正方形,
∴OH⊥CD,△OCD是等腰直角三角形,
∴CH=DH=a,
∵∠AOB=90°,
∴CH=OH,
∴OG=3a,
在Rt△OFG中,OF2=GF2+OG2,即52=a2+(3a)2,
解得a=$\frac{\sqrt{10}}{2}$,
∴CF=2a=$\sqrt{10}$.
故正方形CDEF的边长为$\sqrt{10}$.
故选:C.
点评 本题考查的是垂径定理及勾股定理,解答此题的关键是根据题意画出图形,作出辅助线,构造出直角三角形,再进行解答.

练习册系列答案
相关题目
16.据国家统计局公布,2015年我国国内生产总值约为676700亿元(人民币),请用科学记数法表示数据“676700亿”,结果是( )
| A. | 6.767×105 | B. | 6.676×1012 | C. | 6.676×1013 | D. | 6.676×1014 |
 如图,在平面直角坐标系中有一个平行四边形ABCD.
如图,在平面直角坐标系中有一个平行四边形ABCD. 如图,是根据四边形的不稳定性制作的边长均为20cm的可活动菱形衣架.若墙上钉子间的距离AB=BC=20cm,则∠1=120.
如图,是根据四边形的不稳定性制作的边长均为20cm的可活动菱形衣架.若墙上钉子间的距离AB=BC=20cm,则∠1=120.