Question

16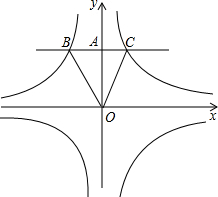．如图，已知反比例函数y=$\frac{k_1}{x}$（k₁＞0），y=$\frac{k_2}{x}$（k₂＜0）．点A在y轴的正半轴上，过点A作直线BC∥x轴，且分别与两个反比例函数的图象交于点B和C，连接OC、OB．若△BOC的面积为$\frac{5}{2}$，AC：AB=2：3，试求这两个反比例函数的表达式．

Answer 1

分析 根据反比例函数系数的几何意义可得，|k₁|+|k₂|的值以及|k₁|：|k₂|的值，然后联立方程组求解得到|k₁|与|k₂|的值，然后即可得解．

解答 解：∵△BOC的面积为$\frac{5}{2}$，
∴$\frac{1}{2}$|k₁|+$\frac{1}{2}$|k₂|=$\frac{5}{2}$，
即|k₁|+|k₂|=5①，
∵AC：AB=2：3，
∴|k₁|：|k₂|=2：3②，
①②联立$\left\{\begin{array}{l}{|{k}_{1}|+|{k}_{2}|=5}\\{|{k}_{1}|：|{k}_{2}|=2：3}\end{array}\right.$，
解得|k₁|=2，|k₂|=3，
∵k₁＞0，k₂＜0，
∴k₁=2，k₂=-3，
∴两个反比例函数的表达式分别为：y=$\frac{2}{x}$，y=-$\frac{3}{x}$．

点评 本题考查了反比例函数系数的几何意义，过双曲线上的任意一点分别向两条坐标作垂线，与坐标轴围成的矩形面积就等于|k|，根据题意得到两个关于反比例函数系数的方程是解题的关键．