题目内容
4.已知(x2+y2)(x2+y2+1)=12,求x2+y2的值.分析 根据换元法解一元二次方程的求解方法,令x2+y2=t,则t(t+1)=12,t≥0;然后根据一元二次方程的求解方法,求出t(t+1)=12的解,即可确定x2+y2的值.
解答 解:令x2+y2=t,
则t(t+1)=12,t≥0,
∴t2+t-12=0,
解得t=3或t=-4(舍去),
即x2+y2的值是3.
点评 此题主要考查了换元法解一元二次方程问题,要熟练掌握,解答此题的关键是要明确:常用的是整体换元法,换元法的实质是转化.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
15.已知a<-1,点(a-1,y1)、(a,y2)、(a+1,y3)都在二次函数y=ax2-3ax+b的图象上,则( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
13.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )
| A. | (2,5) | B. | (-8,5) | C. | (-8,-1) | D. | (2,-1) |

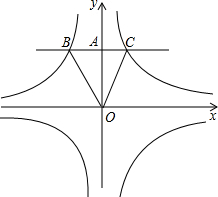 如图,已知反比例函数y=$\frac{k_1}{x}$(k1>0),y=$\frac{k_2}{x}$(k2<0).点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、OB.若△BOC的面积为$\frac{5}{2}$,AC:AB=2:3,试求这两个反比例函数的表达式.
如图,已知反比例函数y=$\frac{k_1}{x}$(k1>0),y=$\frac{k_2}{x}$(k2<0).点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、OB.若△BOC的面积为$\frac{5}{2}$,AC:AB=2:3,试求这两个反比例函数的表达式.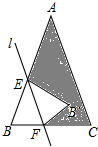 等腰三角形ABC中,顶角A是大于0°小于180°的任意角,直接l∥AC并AB于E,交BC于F,沿直线l折叠角B,点B的对应点为B′,请对以下结论做出判断:
等腰三角形ABC中,顶角A是大于0°小于180°的任意角,直接l∥AC并AB于E,交BC于F,沿直线l折叠角B,点B的对应点为B′,请对以下结论做出判断: