题目内容
12.⊙O中,弦AB、CD相交于圆内的一点P,CP=5cm,DP=9cm,AP:BP=3:5,则AB=8$\sqrt{3}$cm.分析 设AP=3x,BP=5x,根据相交弦定理得到PA•PB=PC•PD,则可计算出AP和BP,即可求得AB.
解答 解:∵弦AB和弦CD相交于⊙O内一点P,
∴PA•PB=PC•PD,
而CP=5cm,DP=9cm,AP:BP=3:5,
设AP=3x,BP=5x,
∴15x2=5×9=45,
∴x2=3,
∴x=$\sqrt{3}$,
∴AP=3$\sqrt{3}$,BP=5$\sqrt{3}$,
∴AB=8$\sqrt{3}$(cm).
故答案为8$\sqrt{3}$.
点评 本题考查了相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等(经过圆内一点引两条线,各弦被这点所分成的两段的积相等).

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 0大于一切非负数 | |
| B. | 数轴上离原点越远,表示的数越大 | |
| C. | 没有最大的正数,却有最大的负数 | |
| D. | 有理数是指正整数、负整数、正分数、负分数、零这五类数 |
7.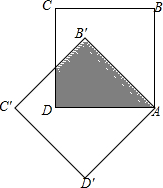 将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )
将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )
 将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )
将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
 如图所示,图中的单位长度为1.
如图所示,图中的单位长度为1. 如图,△ABC与△AEF中,AB=AE,BC=EF,AC=AF,AB交EF于D,求证:DA•DB=DE•DF.
如图,△ABC与△AEF中,AB=AE,BC=EF,AC=AF,AB交EF于D,求证:DA•DB=DE•DF.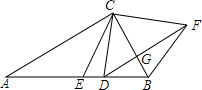 已知:△ABC中,∠ACB=90°,CE是中线,D是AB上的-点,过D作DF∥AC,过B作BF∥EC,DF、BF相交于F.连结CD、CF,求证:CD=CF.
已知:△ABC中,∠ACB=90°,CE是中线,D是AB上的-点,过D作DF∥AC,过B作BF∥EC,DF、BF相交于F.连结CD、CF,求证:CD=CF.