题目内容
19. 如图,△ABC中,BE⊥AC于点E,CF⊥AB于点F,连结EF,若S△ABC=36,S△AEF=16,则$\frac{AE}{AB}$等于( )
如图,△ABC中,BE⊥AC于点E,CF⊥AB于点F,连结EF,若S△ABC=36,S△AEF=16,则$\frac{AE}{AB}$等于( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$或$\frac{2}{3}$ |
分析 由题意可得△ACF∽△ABE,得到$\frac{AE}{AB}=\frac{AF}{AC}$,证得△AEF∽△ACB,再由相似三角形的性质:相似三角形面积比等于相似比的平方即可得出结论.
解答 解:∵BE⊥AC,CF⊥AB,
∴∠AEB=∠AFE=90°,
∵∠A=∠A,
∴△ACF∽△ABE,
∴$\frac{AE}{AB}=\frac{AF}{AC}$,
∴△AEF∽△ACB,
$(\frac{AE}{AB})^{2}$=$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=$\frac{16}{36}$,
∴$\frac{AE}{AB}$=$\frac{2}{3}$,
故选B.
点评 本题主要考查了相似三角形的判定和性质,垂直的定义,熟记相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.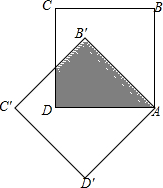 将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )
将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )
 将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )
将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
3.在△ABC中,已知a=1,b=1,c=$\sqrt{3}$,则∠C=( )
| A. | 120° | B. | 30° | C. | 45° | D. | 60° |
4.下列式子中不正确的是( )
| A. | sin60°=$\frac{\sqrt{3}}{2}$ | B. | tan30°•tan60°=1 | ||
| C. | sin230°+cos230°=1 | D. | sin$\frac{1}{2}$=30° |
 如图,△ABC与△AEF中,AB=AE,BC=EF,AC=AF,AB交EF于D,求证:DA•DB=DE•DF.
如图,△ABC与△AEF中,AB=AE,BC=EF,AC=AF,AB交EF于D,求证:DA•DB=DE•DF.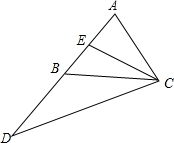 如图,在△ABC中,AC=AB,CE是AB边上的中线,延长AB至D,使BD=AB,问CE与CD有何数量关系?请说明理由.
如图,在△ABC中,AC=AB,CE是AB边上的中线,延长AB至D,使BD=AB,问CE与CD有何数量关系?请说明理由.