题目内容
20. 如图,AB是⊙O的直径,点C在⊙O上,D为AC上一点,BD延长线与⊙O过点A的切线相交于点E,AE=AD.
如图,AB是⊙O的直径,点C在⊙O上,D为AC上一点,BD延长线与⊙O过点A的切线相交于点E,AE=AD.(1)判断BE是否是∠ABC的平分线,并说明理由;
(2)若AB=10,AD=5,求AC长.
分析 (1)结论:BE是∠ABC的角平分线.由∠E+∠ABE=90°,∠CDB+∠DBC=90°,只要证明∠E=∠CDB即可解决问题.
(2)由△CDB∽△AEB,得$\frac{AE}{AB}$=$\frac{CD}{BC}$=$\frac{5}{10}$=$\frac{1}{2}$,设CD=x,BC=2x,则CA=CD+AD=x+5,在Rt△ACB中,由AC2+BC2=AB2,列出方程即可解决问题.
解答 解:(1)结论:BE是∠ABC的角平分线.
理由:∵AD=AE,
∴∠E=∠ADE,
∵∠ADE=∠CDB,
∴∠E=∠CDB,
∵AB是⊙O的直径,点C在⊙O上,
∴∠ACB=90°,
∴∠CDB+∠CBD=90°,
∵AE是切线,
∴AE⊥AB,
∴∠EAB=90°,
∴∠E+∠ABE=90°,
∴∠CBD=∠EBA,
∴BE是∠ABC的平分线.
(2)∵AE=AD,AD=5,
∴AE=AD=5,
∵∠CDB=∠E,∠CBD=∠ABE,
∴△CDB∽△AEB,
∴$\frac{AE}{AB}$=$\frac{CD}{BC}$=$\frac{5}{10}$=$\frac{1}{2}$,设CD=x,BC=2x,则CA=CD+AD=x+5,
在Rt△ACB中,∵AC2+BC2=AB2,
∴(x+5)2+(2x)2=102,
解得x=3或-5(舍弃),
∴AC=5+3=8.
点评 本题从切线的性质、相似三角形判定和性质、等角的余角相等、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会理由参数,用方程的思想思考问题,属于中考常考题型.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
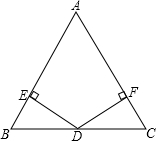 已知:如图,在△ABC中,点D是BC的中点,过点D作DE⊥AB,DF⊥AC,点E,F分别为垂足,且满足BE=CF.求证:AE=AF.
已知:如图,在△ABC中,点D是BC的中点,过点D作DE⊥AB,DF⊥AC,点E,F分别为垂足,且满足BE=CF.求证:AE=AF.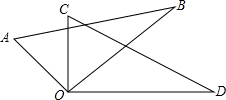 将两个全等的直角三角形如图摆放,若∠AOD=150°,求∠BOC的度数.
将两个全等的直角三角形如图摆放,若∠AOD=150°,求∠BOC的度数.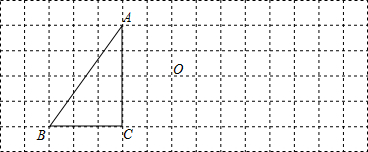
 如图所示,在矩形ABCD中,BC=4,AB=2,P是BC上一动点,动点Q在PC或其延长线上,BP=PQ,四边形PQRS是以PQ为一边的正方形,点P从点B开始沿射线BC方向运动,设BP=x,正方形PQRS与矩形ABCD重叠部分的面积为y.
如图所示,在矩形ABCD中,BC=4,AB=2,P是BC上一动点,动点Q在PC或其延长线上,BP=PQ,四边形PQRS是以PQ为一边的正方形,点P从点B开始沿射线BC方向运动,设BP=x,正方形PQRS与矩形ABCD重叠部分的面积为y.