Question

12．如图所示，在矩形ABCD中，BC=4，AB=2，P是BC上一动点，动点Q在PC或其延长线上，BP=PQ，四边形PQRS是以PQ为一边的正方形，点P从点B开始沿射线BC方向运动，设BP=x，正方形PQRS与矩形ABCD重叠部分的面积为y．
（1）分别求出0≤x≤2和2≤x≤4时，y与x之间的函数关系式；
（2）在同一直角坐标系内画出（1）中所得函数的图象．

Answer 1

分析 （1）分两种情况：①当0≤x≤2时，重合部分为边长是x的正方形，因此y=x²．②当2＜x≤4时，重合部分是个矩形，此矩形相邻两边长分别是（4-x），2，因此此时的函数关系为y=2（4-x）；
（2）根据二次函数与一次函数的图象与性质分别画出图象，注意自变量的取值范围．

解答 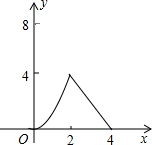解：（1）当0≤x≤2时，y=x²；
当2≤x≤4时，y=2（4-x）；

（2）如图所示：

点评 本题考查了动点问题的函数图象，得到y与x之间的函数关系式是解题的关键．注意自变量的不同得到的函数关系式也不同；有实际意义的函数图象只在第一象限．