题目内容
15.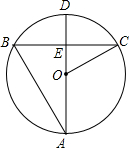 如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC=4$\sqrt{3}$.
如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC=4$\sqrt{3}$.
分析 如图,作辅助线;首先运用勾股定理求出AE的长度,然后运用射影定理求出AD的长度,即可解决问题.
解答  解:如图,连接BD;
解:如图,连接BD;
∵直径AD⊥BC,
∴BE=CE=$\frac{1}{2}$BC=6;
由勾股定理得:
AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=6$\sqrt{3}$;
∵AD为⊙O的直径,
∴∠ABD=90°;
由射影定理得:
AB2=AE•AD
∴AD=$\frac{1{2}^{2}}{6\sqrt{3}}$=8$\sqrt{3}$,
∴OC=$\frac{1}{2}$AD=4$\sqrt{3}$,
故答案为4$\sqrt{3}$.
点评 该题主要考查了垂径定理、射影定理等几何知识点及其应用问题;解题的方法是作辅助线,构造直角三角形;解题的关键是牢固掌握垂径定理、射影定理等几何知识点,这是灵活运用、解题的基础和关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
10.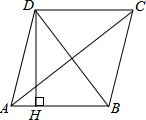 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )| A. | $\frac{24}{5}$ | B. | $\frac{12}{5}$ | C. | 12 | D. | 24 |
7.如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是( )


| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
4.一个多边形的每个内角都等于120°,则这个多边形的边数为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |

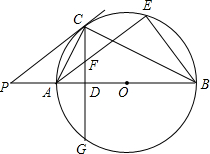 如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D. 某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.