题目内容
3.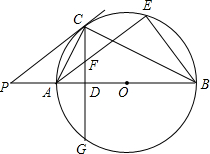 如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.(1)求证:∠PCA=∠ABC;
(2)过点A作AE∥PC,交⊙O于点E,交CD于点F,连接BE.若sin∠P=$\frac{3}{5}$,CF=5,求BE的长.
分析 (1)连接OC,由PC切⊙O于点C,得到OC⊥PC,于是得到∠PCA+∠OCA=90°,由AB为⊙O的直径,得到∠ABC+∠OAC=90°,由于OC=OA,证得∠OCA=∠OAC,于是得到结论;
(2)由AE∥PC,得到∠PCA=∠CAF根据垂径定理得到$\widehat{AC}=\widehat{AG}$,于是得到∠ACF=∠ABC,由于∠PCA=∠ABC,推出∠ACF=∠CAF,根据等腰三角形的性质得到CF=AF,在Rt△AFD中,AF=5,sin∠FAD=$\frac{3}{5}$,求得FD=3,AD=4,CD=8,在Rt△OCD中,设OC=r,根据勾股定理得到方程r2=(r-4)2+82,解得r=10,得到AB=2r=20,由于AB为⊙O的直径,得到∠AEB=90°,在Rt△ABE中,由sin∠EAD=$\frac{3}{5}$,得到$\frac{BE}{AB}=\frac{3}{5}$,于是求得结论.
解答 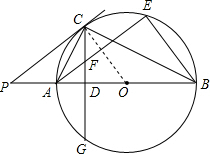 (1)证明:连接OC,
(1)证明:连接OC,
∵PC切⊙O于点C,
∴OC⊥PC,
∴∠PCO=90°,
∴∠PCA+∠OCA=90°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠OAC=90°,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠PCA=∠ABC;
(2)解:∵AE∥PC,
∴∠PCA=∠CAF,
∵AB⊥CG,
∴$\widehat{AC}=\widehat{AG}$,
∴∠ACF=∠ABC,
∵∠PCA=∠ABC,
∴∠ACF=∠CAF,
∴CF=AF,
∵CF=5,
∴AF=5,
∵AE∥PC,
∴∠FAD=∠P,
∵sin∠P=$\frac{3}{5}$,
∴sin∠FAD=$\frac{3}{5}$,
在Rt△AFD中,AF=5,sin∠FAD=$\frac{3}{5}$,
∴FD=3,AD=4,∴CD=8,
在Rt△OCD中,设OC=r,
∴r2=(r-4)2+82,
∴r=10,
∴AB=2r=20,
∵AB为⊙O的直径,
∴∠AEB=90°,在Rt△ABE中,
∵sin∠EAD=$\frac{3}{5}$,∴$\frac{BE}{AB}=\frac{3}{5}$,
∵AB=20,
∴BE=12.
点评 本题考查了切线的性质,锐角三角函数,圆周角定理,等腰三角形的性质,连接OC构造直角三角形是解题的关键.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )| A. | 68° | B. | 88° | C. | 90° | D. | 112° |
| 品牌 | 进价/(元/件) | 售价/(元/件) |
| A | 50 | 80 |
| B | 40 | 65 |
(2)如果购进两种T恤的总费用不超过9500元,那么超市如何进货才能获得最大利润?并求出最大利润.(提示:利润=售价-进价)
 如图是一个几何体的三视图,则这个几何体是( )
如图是一个几何体的三视图,则这个几何体是( )| A. | 正方体 | B. | 长方体 | C. | 三棱柱 | D. | 三棱锥 |
| A. | 4,4 | B. | 3,4 | C. | 4,3 | D. | 3,3 |
 如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的值为( )
如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的值为( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
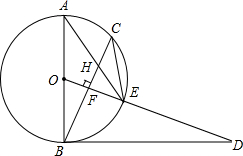 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC. 如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC=4$\sqrt{3}$.
如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC=4$\sqrt{3}$.