题目内容
20. 某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)首先求得某顾客参加一次抽奖,能获得返还现金的情况,再利用概率公式即可求得答案.
解答 解:(1)画树状图得:
则共有16种等可能的结果;
(2)∵某顾客参加一次抽奖,能获得返还现金的有6种情况,
∴某顾客参加一次抽奖,能获得返还现金的概率是:$\frac{6}{16}$=$\frac{3}{8}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
10.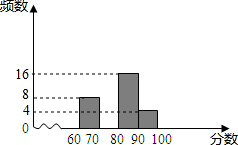 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图
请根据图表提供的信息,解答下列问题:
(1)表中的a=12,b=40;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是108°;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为$\frac{2}{3}$.
 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图| 分数段(分手为x分) | 频数 | 百分比 |
| 60≤x<70 | 8 | 20% |
| 70≤x<80 | a | 30% |
| 80≤x≤90 | 16 | b% |
| 90≤x<100 | 4 | 10% |
(1)表中的a=12,b=40;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是108°;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为$\frac{2}{3}$.
8.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的平均数、中位数分别是( )
| A. | 4,4 | B. | 3,4 | C. | 4,3 | D. | 3,3 |
5.用配方法解一元二次方程x2-6x-4=0,下列变形正确的是( )
| A. | (x-6)2=-4+36 | B. | (x-6)2=4+36 | C. | (x-3)2=-4+9 | D. | (x-3)2=4+9 |
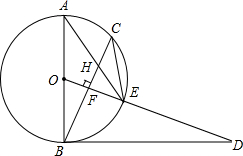 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.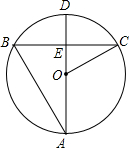 如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC=4$\sqrt{3}$.
如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC=4$\sqrt{3}$.