题目内容
10．
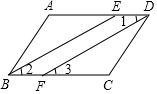如图，在?ABCD中，BE，DF分别平分∠ABC，∠ADC．求证：BE∥DF．
分析 利用平行四边形的性质结合角平分线的性质得出∠ABE=∠AEB，∠CFD=∠CDF，进而得出∠AEB=∠ADF，即可得出答案．
解答 证明：∵四边形ABCD式平行四边形，
∴AD∥BC，∠ABC=∠ADC，
∵BE、DF分别平分∠ABC、∠ADC，
∴∠ABE=∠CBE，∠AEB=∠CBE，∠CDF=∠ADF，∠CFD=∠ADF，
∴∠ABE=∠AEB，∠CFD=∠CDF，
又∵∠ABC=∠ADC，
∴∠AEB=∠ADF，
∴BE∥DF．
点评 此题主要考查了平行四边形的性质以及角平分线的性质，得出∠AEB=∠ADF是解题关键．
练习册系列答案
巧学巧练系列答案
相关题目
9．
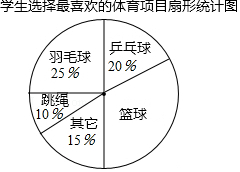某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查，调查的运动项目有：篮球、羽毛球、乒乓球、跳绳及其它项目（每位同学仅选一项），根据调查数据绘制了如下不完整的统计表和扇形统计图：
学生选择最喜爱的体育项目统计表
请根据以上图表信息解答下列问题：
（1）统计表中的m=30，n=0.20；
（2）在扇形统计图中，“篮球”所在扇形的圆心角为108度；
（3）该学校共有2400名学生，据此估计有多少名学生最喜爱乒乓球？
（4）将2名最喜爱篮球的学生和2名最喜爱羽毛球的学生编为一组，从中随机抽取两人，请用列表或画树状图的方法求出所抽取的两人都选择了最喜爱篮球的概率．
某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查，调查的运动项目有：篮球、羽毛球、乒乓球、跳绳及其它项目（每位同学仅选一项），根据调查数据绘制了如下不完整的统计表和扇形统计图：学生选择最喜爱的体育项目统计表
| 运动项目 | 频数（人数） | 频率 |
| 篮球 | 36 | 0.30 |
| 羽毛球 | m | 0.25 |
| 乒乓球 | 24 | n |
| 跳绳 | 12 | 0.10 |
| 其它项目 | 18 | 0.15 |
（1）统计表中的m=30，n=0.20；
（2）在扇形统计图中，“篮球”所在扇形的圆心角为108度；
（3）该学校共有2400名学生，据此估计有多少名学生最喜爱乒乓球？
（4）将2名最喜爱篮球的学生和2名最喜爱羽毛球的学生编为一组，从中随机抽取两人，请用列表或画树状图的方法求出所抽取的两人都选择了最喜爱篮球的概率．