题目内容
2.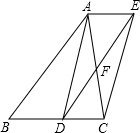 如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F.
如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F.(1)求证:四边形ADCE是平行四边形;
(2)如果四边形ADCE是矩形,△ABC应满足什么条件?并说明理由.
分析 (1)证出四边形ABDE是平行四边形,得出AE=BD,由已知得出AE=CD,即可得出四边形ADCE是平行四边形.
(2)由矩形的性质得出∠ADB=90°,由线段垂直平分线的性质得出AB=AC即可.
解答 (1)证明:∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵点D是△ABC的边BC的中点,
∴BD=CD,
∴AE=CD,
∴四边形ADCE是平行四边形.
(2)解:如果四边形ADCE是矩形,△ABC是等腰三角形;理由如下:
∵四边形ADCE是矩形,
∴∠ADC=90°,
∴∠ADB=90°,即AD⊥BC,
∵点D是△ABC的边BC的中点,
∴AB=AC,
即△ABC是等腰三角形.
点评 此题主要考查了矩形的性质、平行四边形的判定与性质、线段垂直平分线的性质;熟练掌握平行四边形的判定与性质是解题关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
12.为了考查甲、乙两种小麦的长势,分别从中随机抽取10株麦苗,测得苗高(单位:cm)如表:
(1)分别计算两种小麦的平均苗高;
(2)哪种小麦的长势比较整齐?并说明理由.
| 甲 | 16 | 18 | 18 | 19 | 20 | 20 | 21 | 21 | 23 | 24 |
| 乙 | 13 | 15 | 17 | 18 | 20 | 21 | 23 | 23 | 24 | 26 |
(2)哪种小麦的长势比较整齐?并说明理由.
10.如果一个四边形的两条对角线相等且互相平分,那么这个四边形是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 平行四边形 |
17.下列四个多项式中,不能因式分解的是( )
| A. | a2+1 | B. | a2-6a+9 | C. | x2+5x | D. | x2-y2 |
 某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.