题目内容
7.计算:(1)$\frac{5}{6}$+(-1$\frac{2}{3}$)-(-1)
(2)-22+$\root{3}{27}$-6+(-2)×$\sqrt{9}$.
分析 (1)先化简,再计算加减法;
(2)本题涉及二次根式化简、三次根式化简2个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答 解:(1)$\frac{5}{6}$+(-1$\frac{2}{3}$)-(-1)
=$\frac{5}{6}$-1$\frac{2}{3}$+1
=$\frac{1}{6}$;
(2)-22+$\root{3}{27}$-6+(-2)×$\sqrt{9}$
=-4+3-6-6
=-13.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握二次根式、三次根式等考点的运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17. 甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )
甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )
 甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )
甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )| A. | 货车的速度是60千米/小时 | |
| B. | 离开出发地后,两车第一次相遇时,距离出发地150千米 | |
| C. | 货车从出发地到终点共用时7小时 | |
| D. | 客车到达终点时,两车相距180千米 |
12.某汽车专卖店计划购进甲、乙两种新型汽车共140辆,这两种汽车的进价、售价如下表:
(1)若该汽车专卖店投入1000万元资金进货,则购进甲乙两种新型汽车各多少辆?
(2)若该汽车专卖店准备乙种型号汽车的进货量不超过甲种型号汽车的进货量的3倍,应怎样安排进货方案,才能使该汽车专卖店售完这两种新型汽车后获得的利润最大?最大利润是多少?(其它成本不计)
| 进价(万元/辆) | 售价(万元/辆) | |
| 甲 | 5 | 8 |
| 乙 | 9 | 13 |
(2)若该汽车专卖店准备乙种型号汽车的进货量不超过甲种型号汽车的进货量的3倍,应怎样安排进货方案,才能使该汽车专卖店售完这两种新型汽车后获得的利润最大?最大利润是多少?(其它成本不计)
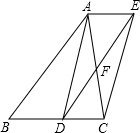 如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F.
如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F. 如图,电信部门要在两条公路之间及海岸线围城的S区域内修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路的距离也必须相等.发射塔P建在什么位置?
如图,电信部门要在两条公路之间及海岸线围城的S区域内修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路的距离也必须相等.发射塔P建在什么位置? 如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.请证明:四边形EGFH是平行四边形.
如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.请证明:四边形EGFH是平行四边形. 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,