题目内容
13. 某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.(1)试判断△BCD的形状;
(2)若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
分析 仔细分析题目,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解.
解答 (1)解:△BCD是直角三角形;理由如下:
∵∠A=90°,AB=3,AD=4,BC=12,
根据勾股定理得BD2=AB2+AD2=32+42=25,
∴BD2+BC2=25+144=169=132=CD2,
根据勾股定理的逆定理,
∴∠CBD=90°
∴△BCD是直角三角形.
(2)四边形ABCD的面积=${S_{△ABD}}+{S_{△BCD}}=\frac{1}{2}×3×4+\frac{1}{2}×5×12$=6+30=36m2
∴学校要投入资金为:200×36=7200元;
答:学校需要投入7200元买草皮.
点评 本题考查了勾股定理、勾股定理的逆定理的应用,通过勾股定理由边与边的关系也可证明直角三角形,这样解题较为简单.

练习册系列答案
相关题目
1.在下列对称图形中,对称轴的条数最多的图形是( )
| A. | 圆 | B. | 等边三角形 | C. | 正方形 | D. | 正六边形 |
5. 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$=( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$=( )
 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$=( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$=( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{5}$ | D. | $\frac{5}{3}$ |
3.两个多边形相似的条件是( )
| A. | 对应角相等 | B. | 对应角相等且对应边成比例 | ||
| C. | 对应角相等或对应边成比例 | D. | 对应边成比例 |
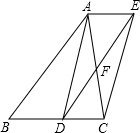 如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F.
如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F. 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,