题目内容
7. 如图,在⊙O中,直径AB=10,弦CD⊥AB,垂足为E,OE=3,求弦CD的长.
如图,在⊙O中,直径AB=10,弦CD⊥AB,垂足为E,OE=3,求弦CD的长.
分析 连接OC,先根据垂径定理得出CD=2CE,再由勾股定理求出CE的长即可.
解答  解:连接OC,
解:连接OC,
∵直径AB=10,
∴OC=5.
∵弦CD⊥AB,垂足为E,OE=3,
∴CD=2CE,CE=$\sqrt{{OC}^{2}-{OE}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴CD=8.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
2.元旦期间,为了满足长丰县百姓的消费需要,某大型商场计划用170000元购进一批家电,这批家里的进价和售价如表:
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商场购买冰箱x台.
(1)用含x的代数式表示洗衣机的台数.
(2)商场至多可以购买冰箱多少台?
(3)购买冰箱多少台时,能使商场销售完这批家电后获得的利润最大?最大利润为多少元?
| 类别 | 彩电 | 冰箱 | 洗衣机 |
| 进价(元/台) | 2000 | 1600 | 1000 |
| 售价(元/台) | 2300 | 1800 | 1100 |
(1)用含x的代数式表示洗衣机的台数.
(2)商场至多可以购买冰箱多少台?
(3)购买冰箱多少台时,能使商场销售完这批家电后获得的利润最大?最大利润为多少元?
12.两种移动电话计费方式表如下:
(1)一个月内某用户在本地通话时间为x分钟,请你用含有x的式子分别写出两种计费方式下该用户应该支付的费用.
(2)若某用户一个月内本地通话时间为5个小时,你认为采用哪种方式较为合算?
| 全球通 | 神州行 | |
| 月租费 | 15元/月 | 0 |
| 本地通话费 | 0.10元/分 | 0.20元/分 |
(2)若某用户一个月内本地通话时间为5个小时,你认为采用哪种方式较为合算?
16.下列图形中不是中心对称图形的为( )
| A. | 正方形 | B. | 正五边形 | C. | 正六边形 | D. | 正八边形 |
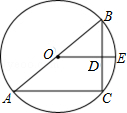 如图,AB是⊙O的直径,BC是弦,点E是BC的中点,OE交BC于点D.连接AC,若BC=6,DE=1,求AC的长.
如图,AB是⊙O的直径,BC是弦,点E是BC的中点,OE交BC于点D.连接AC,若BC=6,DE=1,求AC的长. 如图,经过平移,将的顶点A移到了点D,请作出平移后图形.
如图,经过平移,将的顶点A移到了点D,请作出平移后图形.