题目内容
在数学的学习过程中,我们经常用一下的探索过程解决相关问题数学问题:平面内有1个点,如果在平面内再添加n个点,并过这n+1个点中任意两点画直线,那么最多可以画出多少条直线?
| 添加点的个数 | 图形 | 最多可画出的直线条数 |
| 1 |  | 1 |
| 2 | 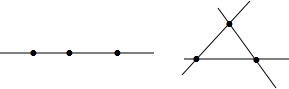 | 3 |
| 3 | 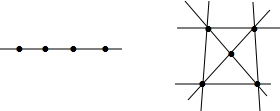 | ? |
| … | … | … |
考点:规律型:图形的变化类
专题:
分析:因为经过任何两点的直线都不重合时最多,经过每个点的直线一定有n-1条,因此n个点共n(n-1)条,但每两个点之间的连线重复,因此要把总条数乘
,即总条数是
n(n-1)条,由此规律得出答案即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:平面内有1个点,如果在平面内再添加1个点,并过这2个点可以画一条直线;
平面内有1个点,如果在平面内再添加2个点,并过这3个点最多可以画
×3×(3-1)=3条直线;
平面内有1个点,如果在平面内再添加3个点,并过这4个点最多可以画
×4×(4-1)=6条直线;
…
平面内有1个点,如果在平面内再添加n个点,并过这n+1个点中任意两点画直线,那么最多可以画出
n(n+1)条直线.
平面内有1个点,如果在平面内再添加2个点,并过这3个点最多可以画
| 1 |
| 2 |
平面内有1个点,如果在平面内再添加3个点,并过这4个点最多可以画
| 1 |
| 2 |
…
平面内有1个点,如果在平面内再添加n个点,并过这n+1个点中任意两点画直线,那么最多可以画出
| 1 |
| 2 |
点评:此题考查图形的变化规律,从简单的情形入手,找出规律,利用规律解决问题.

练习册系列答案
相关题目
 如图,在山坡上种树,要求株距(相邻两树间的水平距离)是5.5m,测得斜坡的倾斜角是24°,求斜坡上两树间的坡面距离(结果保留小数点后一位).
如图,在山坡上种树,要求株距(相邻两树间的水平距离)是5.5m,测得斜坡的倾斜角是24°,求斜坡上两树间的坡面距离(结果保留小数点后一位).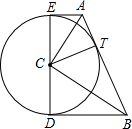 以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A,B分别作⊙C的切线,E,D为切点.求证:
以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A,B分别作⊙C的切线,E,D为切点.求证: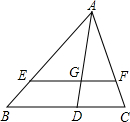 如图,在△ABC中,AD是高,点E在AB上,EF∥BC,分别交AC、AD于点F、G,且
如图,在△ABC中,AD是高,点E在AB上,EF∥BC,分别交AC、AD于点F、G,且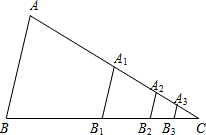 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为