题目内容
在△ABC中,若∠A、∠B满足|tanA-
|+(sinB-
)2=0,则∠C= .
| 3 |
| ||
| 2 |
考点:特殊角的三角函数值
专题:
分析:根据绝对值的性质以及偶次方的性质结合特殊角的三角函数值得出答案.
解答:解:∵|tanA-
|+(sinB-
)2=0,
∴tanA-
=0,sinB-
=0,
解得:∠A=60°,∠B=60°,
∴∠C=60°.
故答案为:60°.
| 3 |
| ||
| 2 |
∴tanA-
| 3 |
| ||
| 2 |
解得:∠A=60°,∠B=60°,
∴∠C=60°.
故答案为:60°.
点评:此题主要考查了特殊角的三角函数值,正确记忆相关角度的三角函数值是解题关键.

练习册系列答案
相关题目
 已知△ABC中,∠C=90°,∠B=60°.
已知△ABC中,∠C=90°,∠B=60°.

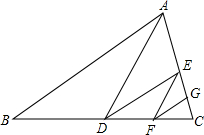 如图,AD是△ABC的中线,DE是△ADC的中线,EF是△DEC的中线,FG是△EFC的中线.
如图,AD是△ABC的中线,DE是△ADC的中线,EF是△DEC的中线,FG是△EFC的中线. 如图所示,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,求作Rt△ABC的内切圆并求出△ABC内切圆的半径.
如图所示,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,求作Rt△ABC的内切圆并求出△ABC内切圆的半径.