题目内容
等边△ABC的边长为4cm，两个动点M、N同时从顶点A出发，点M沿线段AB-BC向点C运动，速度为2cm/s，点N沿线段AC向点C运动，速度为1cm/s，当运动的时间为 s时，两动点M、N首次相遇，相遇的位置是 ．
考点：一元一次方程的应用,等边三角形的性质
专题：几何动点问题
分析：设运动xs时，两动点M、N首次相遇，根据首次相遇时两动点总共走的路程为12cm列出方程，求出方程的解即可得到结果．
解答：解：设运动xs时，两动点M、N首次相遇，
根据题意得：（1+2）x=12，
解得：x=4，
则运动4s时，两动点M、N相遇，且相遇位置为点C，
故答案为：4；点C
根据题意得：（1+2）x=12，
解得：x=4，
则运动4s时，两动点M、N相遇，且相遇位置为点C，
故答案为：4；点C
点评：此题考查了一元一次方程的应用，以及等边三角形的性质，熟练掌握相遇问题的性质是解本题的关键．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
相关题目
如图，已知∠APC、∠BPD都是直角，∠APD=110°，求∠BPC的度数．
一个函数的图象是双曲线（如图），根据图象，求出这个函数的解析式和m的值．
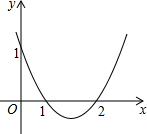如图，抛物y=x2+bx+c与x轴交于点（1，0）、（2，0），x1、x2是关于x的方程x2+bx+c=0的两个根，则x1+x2=