题目内容
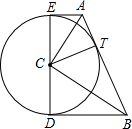 以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A,B分别作⊙C的切线,E,D为切点.求证:
以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A,B分别作⊙C的切线,E,D为切点.求证:(1)BC+AE=AB;
(2)BD∥AE.
考点:切线的性质
专题:证明题
分析:(1)根据切线长定理由AE和AT为⊙O的切线得到AE=AT,由BD和BT为⊙O的切线得BD=BT,则AE+BD=AT+BT=AB;
(2)根据切线长定理得∠CAE=∠CAT,∠CBD=∠CBT,则∠CAB+∠CBA=90°,所以∠CAE+∠CAT+∠CBD+∠CBT=180°,即∠EAB+∠DBA=180°,于是可根据平行线的判定得到BD∥AE.
(2)根据切线长定理得∠CAE=∠CAT,∠CBD=∠CBT,则∠CAB+∠CBA=90°,所以∠CAE+∠CAT+∠CBD+∠CBT=180°,即∠EAB+∠DBA=180°,于是可根据平行线的判定得到BD∥AE.
解答:证明:(1)∵AE和AT为⊙O的切线,
∴AE=AT,
∵BD和BT为⊙O的切线,
∴BD=BT,
∴AE+BD=AT+BT,
即BD+AE=AB;
(2)∵AE和AT为⊙O的切线,
∴∠CAE=∠CAT,
∵BD和BT为⊙O的切线,
∴∠CBD=∠CBT,
∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
∴∠CAE+∠CAT+∠CBD+∠CBT=180°,
即∠EAB+∠DBA=180°,
∴BD∥AE.
∴AE=AT,
∵BD和BT为⊙O的切线,
∴BD=BT,
∴AE+BD=AT+BT,
即BD+AE=AB;
(2)∵AE和AT为⊙O的切线,
∴∠CAE=∠CAT,
∵BD和BT为⊙O的切线,
∴∠CBD=∠CBT,
∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
∴∠CAE+∠CAT+∠CBD+∠CBT=180°,
即∠EAB+∠DBA=180°,
∴BD∥AE.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了切线长定理和平行线的判定.

练习册系列答案
相关题目
 如图是平放在桌面上的长方体木块,其长为14cm,宽为10cm,高为20cm,点B是高CD的中点,一只蜘蛛要沿长方体木块的表面从A点爬到B点,请你求出蜘蛛爬行的最短路程是多少?
如图是平放在桌面上的长方体木块,其长为14cm,宽为10cm,高为20cm,点B是高CD的中点,一只蜘蛛要沿长方体木块的表面从A点爬到B点,请你求出蜘蛛爬行的最短路程是多少?

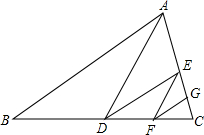 如图,AD是△ABC的中线,DE是△ADC的中线,EF是△DEC的中线,FG是△EFC的中线.
如图,AD是△ABC的中线,DE是△ADC的中线,EF是△DEC的中线,FG是△EFC的中线. 如图中,直角三角形中未知边x的长度为:x=
如图中,直角三角形中未知边x的长度为:x=