题目内容
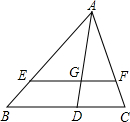如图，在△ABC中，AD是高，点E在AB上，EF∥BC，分别交AC、AD于点F、G，且| BC |
| EF |
| 5 |
| 3 |
（1）
| AD |
| AG |
（2）△AEF与△ABC的面积比．
考点：相似三角形的判定与性质
专题：
分析：（1）易证△AEF∽△ABC，
=
，即可求得
=
，即可解题；
（2）根据相似三角形面积的比值等于相似比的平方即可解题．
| AF |
| AC |
| AG |
| AD |
| AG |
| AD |
| EF |
| BC |
（2）根据相似三角形面积的比值等于相似比的平方即可解题．
解答：解：（1）∵EF∥BC，
∴△AEF∽△ABC，
=
，
∴
=
，
∴
=
，
∴
=
=
；
（2）∵△AEF∽△ABC，
∴△AEF与△ABC的面积比=(
)2=
．
∴△AEF∽△ABC，
| AF |
| AC |
| AG |
| AD |
∴
| AF |
| AC |
| EF |
| BC |
∴
| AG |
| AD |
| EF |
| BC |
∴
| AD |
| AG |
| BC |
| EF |
| 5 |
| 3 |
（2）∵△AEF∽△ABC，
∴△AEF与△ABC的面积比=(
| EF |
| BC |
| 9 |
| 25 |
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，考查了相似三角形面积比等于相似比平方得性质，本题中求证△AEF∽△ABC是解题的关键．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
如图，AD是△ABC的中线，DE是△ADC的中线，EF是△DEC的中线，FG是△EFC的中线．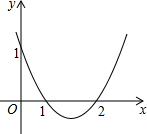
如图，抛物y=x2+bx+c与x轴交于点（1，0）、（2，0），x1、x2是关于x的方程x2+bx+c=0的两个根，则x1+x2=
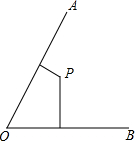已知∠AOB=60°，P为角内部一点，P到OA、OB的距离分别为1和5，在射线OA上找一点M，在射线OB上找一点N，使PM+PN最小，则最小值为