题目内容
19.函数y=ax2+bx+a+b(a≠0)的图象可能是( )| A. | 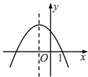 | B. | 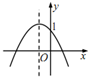 | C. |  | D. | 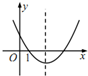 |
分析 根据各选项中函数的图象可以得到a、b、c的关系,从而可以判断各选项中那个函数图象可能是正确的.
解答 解:A:由图象可知,开口向下,则a<0,又因为顶点在y轴左侧,则b<0,则a+b<0,而图象与y轴交点为(0,a+b)在y轴正半轴,与a+b<0矛盾,故此选项错误;
B:由图象可知,开口向下,则a<0,又因为顶点在y轴左侧,则b<0,则a+b<0,而图象与y轴交点为(0,1)在y轴正半轴,可知a+b=1与a+b<0矛盾,故此选项错误;
C:由图象可知,开口向上,则a>0,顶点在y轴右侧,则b<0,a+b=1,故此选项正确;
D:由图象可知,开口向上,则a>0,顶点在y轴右侧,则b<0,与y轴交于正半轴,则a+b>0,而图象与x轴的交点为(1,0),则a+b+a+b=0,即a+b=0与a+b>0矛盾,故此选项错误.
故选C.
点评 本题考查二次函数的图象,解题的关键是明确二次函数的性质,由函数图象可以判断a、b、c的关系.

练习册系列答案
相关题目
9.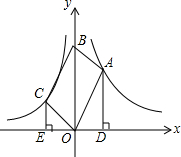 在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
 在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )| A. | 4:9 | B. | 2:3 | C. | 3:2 | D. | 9:4 |
8.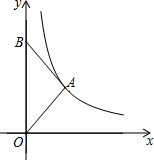 如图,在平面直角坐标系中,点B在y轴上,第一象限内点A满足AB=AO,反比例函数y=$\frac{k}{x}$的图象经过点A,若△ABO的面积为2,则k的值为( )
如图,在平面直角坐标系中,点B在y轴上,第一象限内点A满足AB=AO,反比例函数y=$\frac{k}{x}$的图象经过点A,若△ABO的面积为2,则k的值为( )
 如图,在平面直角坐标系中,点B在y轴上,第一象限内点A满足AB=AO,反比例函数y=$\frac{k}{x}$的图象经过点A,若△ABO的面积为2,则k的值为( )
如图,在平面直角坐标系中,点B在y轴上,第一象限内点A满足AB=AO,反比例函数y=$\frac{k}{x}$的图象经过点A,若△ABO的面积为2,则k的值为( )| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{1}{2}$ |
 如图,已知抛物线y=ax2+$\frac{5}{2}$x+c经过A(4,0),B(1,0)两点,
如图,已知抛物线y=ax2+$\frac{5}{2}$x+c经过A(4,0),B(1,0)两点, 已知:如图,B,A,E在同一直线上,AC∥BD且AC=BE,∠ABC=∠D.求证:AB=BD.
已知:如图,B,A,E在同一直线上,AC∥BD且AC=BE,∠ABC=∠D.求证:AB=BD. 如图,⊙O的半径是2,∠ACB=30°,则小扇形AOB的面积是$\frac{2}{3}$π(结果保留π).
如图,⊙O的半径是2,∠ACB=30°,则小扇形AOB的面积是$\frac{2}{3}$π(结果保留π).