题目内容
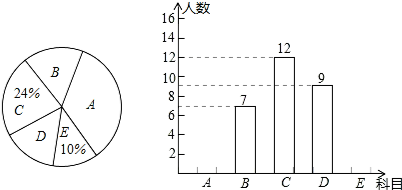
11.某校社团活动开设的体育选修课有:篮球(A),足球(B),排球(C),羽毛球(D),乒乓球(E),每个学生选修其中的一门,学校对某班全班同学的选课情况进行调查统计后制成了以下两个统计图.(1)请你求出该班的总人数,并补全频数分布直方图;
(2)该班的其中某4个同学,1人选修篮球(A),2人选修足球(B),1人选修排球(C).若要从这4人中选2人,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
分析 (1)利用A组的人数除以它所占的百分比即可得到总人数,再计算出E组人数,然后计算出A组人数后补全频数分布直方图;
(2)利用列表法展示所有12种等可能的结果数,再找出选出的2人恰好1人选修篮球,1人选修足球的结果数,然后根据概率公式求解.
解答 解:(1)总人数=12÷24%=50(人),E的人数=50×10%=5(人),
所以A的人数=50-7-12-9-5=17(人),
频数分布直方图为:
(2)列表如下:
| 第一个人选修 第二个人选修 | A | B | B | C |
| A | AB | AB | AC | |
| B | AB | BB | BC | |
| B | AB | BB | BC | |
| C | AC | BC | BC |
所以选出的2人恰好1人选修篮球,1人选修足球的概率=$\frac{4}{12}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了统计图.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.“中华人民共和国全国人民代表大会”和“中国人民政治协商会议”于2016年3月3日在北京胜利召开.截止到2016年3月14日,在百度上搜索关键词“两会”,显示的搜索结果约为96 500 000条.将96 500 000用科学记数法表示应为( )
| A. | 96.5×107 | B. | 9.65×107 | C. | 9.65×108 | D. | 0.965×109 |
19.函数y=ax2+bx+a+b(a≠0)的图象可能是( )
| A. | 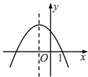 | B. | 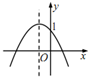 | C. |  | D. | 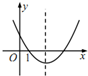 |
6. 实数a,b在数轴上的位置如图所示,下列结论中正确的是( )
实数a,b在数轴上的位置如图所示,下列结论中正确的是( )
 实数a,b在数轴上的位置如图所示,下列结论中正确的是( )
实数a,b在数轴上的位置如图所示,下列结论中正确的是( )| A. | a>b | B. | |a|>|b| | C. | -a<b | D. | a+b<0 |
20.若方程x2-3x-4=0的两根分别为x1和x2,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值是( )
| A. | 1 | B. | 2 | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
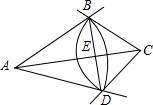 如图,在△ABC中,按如下步骤作图:
如图,在△ABC中,按如下步骤作图: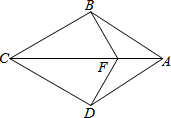 如图,在四边形ABCD中,AB=AD,CB=CD,点F是AC上一点,连结BF,DF.
如图,在四边形ABCD中,AB=AD,CB=CD,点F是AC上一点,连结BF,DF.