题目内容
10. 如图,已知抛物线y=ax2+$\frac{5}{2}$x+c经过A(4,0),B(1,0)两点,
如图,已知抛物线y=ax2+$\frac{5}{2}$x+c经过A(4,0),B(1,0)两点,(1)求该抛物线的解析式;
(2)在直线AC上方的该抛物线上是否存在一点D,使得△DCA的面积最大?若存在,求出点D的坐标及△DCA面积的最大值;若不存在,请说明理由.
分析 (1)把A与B坐标代入抛物线解析式求出a与c的值,即可确定出抛物线解析式;
(2)存在,理由为:如图,设D横坐标为t,代入抛物线解析式表示出纵坐标,过D作y轴的平行线交AC于E,连接CD,AD,如图所示,利用待定系数法确定出直线AC解析式,表示出E坐标,进而表示出DE长,三角形DAC面积等于DE与OA积的一半,利用二次函数性质求出S的最大值,确定出此时D坐标即可.
解答  解:(1)把A(4,0),B(1,0)代入抛物线的解析式得:$\left\{\begin{array}{l}{0=16a+10+c}\\{a+\frac{5}{2}+c=0}\end{array}\right.$,
解:(1)把A(4,0),B(1,0)代入抛物线的解析式得:$\left\{\begin{array}{l}{0=16a+10+c}\\{a+\frac{5}{2}+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=-2}\end{array}\right.$,
则抛物线解析式为y=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2;
(2)存在,理由如下:
设D的横坐标为t(0<t<4),则D点的纵坐标为-$\frac{1}{2}$t2+$\frac{5}{2}$t-2,
过D作y轴的平行线交AC于E,连接CD,AD,如图所示,
由题意可求得直线AC的解析式为y=$\frac{1}{2}$x-2,
∴E点的坐标为(t,$\frac{1}{2}$t-2),
∴DE=-$\frac{1}{2}$t2+$\frac{5}{2}$t-2-($\frac{1}{2}$t-2)=-$\frac{1}{2}$t2+2t,
∴△DAC的面积S=$\frac{1}{2}$×(-$\frac{1}{2}$t2+2t)×4=-t2+4t=-(t-2)2+4,
当t=2时,S最大=4,
∴此时D(2,1),△DAC面积的最大值为4.
点评 此题考查了待定系数法确定二次函数解析式,以及二次函数的最值,熟练掌握待定系数法是解本题的关键.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案| A. | 96.5×107 | B. | 9.65×107 | C. | 9.65×108 | D. | 0.965×109 |
| A. | 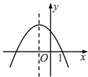 | B. | 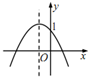 | C. |  | D. | 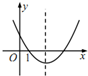 |
| A. | 1 | B. | 2 | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
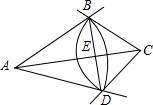 如图,在△ABC中,按如下步骤作图:
如图,在△ABC中,按如下步骤作图: