题目内容
9.不等式组$\left\{\begin{array}{l}{2x+1>-3}\\{-x+3≥0}\end{array}\right.$的解集为-2<x≤3.分析 利用不等式的性质,先求出两个不等式的解集,再求其公共解.
解答 解:$\left\{\begin{array}{l}{2x+1>-3①}\\{-x+3≥0②}\end{array}\right.$,
由①式得x>-2;
由②式得x≤3,
所以不等式组的解为-2<x≤3,
故答案为-2<x≤3.
点评 此题考查解不等式组;求不等式组的解集,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
19.函数y=ax2+bx+a+b(a≠0)的图象可能是( )
| A. |  | B. | 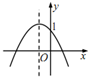 | C. |  | D. | 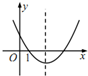 |
20.若方程x2-3x-4=0的两根分别为x1和x2,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值是( )
| A. | 1 | B. | 2 | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
14.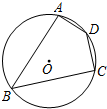 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )| A. | π | B. | 2π | C. | 4π | D. | 8π |