题目内容
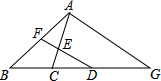如图，已知△ABG∽△FBD，△CDE∽△CGA，F是AB的中点，说明：| BD |
| CD |
| AE |
| EC |
考点：相似三角形的性质
专题：证明题
分析：根据相似三角形对应角相等可得∠G=∠BDF，然后根据同位角相等，两直线平行判断出DF∥AC，从而判断出DF是△ABG的中位线，然后求出BD=DG，再根据平行线分线段成比例定理证明即可．
解答：证明：∵△ABG∽△FBD，
∴∠G=∠BDF，
∴DF∥AC，
∵F是AB的中点，
∴DF是△ABG的中位线，
∴BD=DG，
又∵DF∥AC，
∴
=
，
∴
=
．
∴∠G=∠BDF，
∴DF∥AC，
∵F是AB的中点，
∴DF是△ABG的中位线，
∴BD=DG，
又∵DF∥AC，
∴
| DG |
| CD |
| AE |
| EC |
∴
| BD |
| CD |
| AE |
| EC |
点评：本题考查了相似三角形对应角相等的性质，平行线分线段成比例定理，三角形的中位线的判定，根据对应顶点的字母写在对应位置上准确确定出对应角是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知双曲线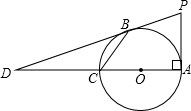
如图所示，AC为⊙O的直径且PA⊥AC，BC是⊙O的一条弦，直线PB交直线AC于点D，且
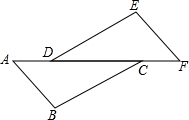如图，△ABC与△DEF的点A、D、C、F在同一直线上，且AD=CF，BC=ED，∠BCA=∠EDF．
如图，两个同心圆都以O点为圆心，大圆的弦AB交小圆于C、D两点，若AB=3cm，CD=2cm，求圆环的面积．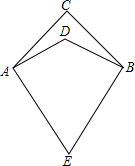
如图，D是四边形AEBC内一点，连接AD、BD，已知CA=CB，DA=DB，EA=EB．