题目内容
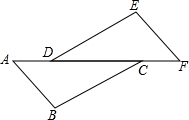如图，△ABC与△DEF的点A、D、C、F在同一直线上，且AD=CF，BC=ED，∠BCA=∠EDF．（1）证明：△ABC≌△FED；
（2）你还能证得其他新的结论吗？
考点：全等三角形的判定与性质
专题：证明题
分析：（1）先求出AC=FD，再利用“边角边”证明△ABC和△FED全等即可；
（2）根据全等三角形对应角相等，全等三角形对应边相等解答．
（2）根据全等三角形对应角相等，全等三角形对应边相等解答．
解答：（1）证明：∵AD=CF，
∴AD+CD=CF+CD，
即AC=FD，
在△ABC和△FED中，
，
∴△ABC≌△FED（SAS）；
（2）∵△ABC≌△FED，
∴∠A=∠F，∠B=∠E，AB=EF（写任意一个即可）．
∴AD+CD=CF+CD，
即AC=FD，
在△ABC和△FED中，
|
∴△ABC≌△FED（SAS）；
（2）∵△ABC≌△FED，
∴∠A=∠F，∠B=∠E，AB=EF（写任意一个即可）．
点评：本题考查了全等三角形的判定与性质，比较简单，熟记三角形全等的判定方法并求出AC=FD是解题的关键．
练习册系列答案
相关题目
能够判别一个四边形是平行四边形的条件是（ ）
| A、一组对角相等 |
| B、两条对角线互相垂直且相等 |
| C、两组对边分别相等 |
| D、一组对边平行 |
如图，已知△ABC中，AB的垂直平分线交BC于D，AC的垂直平分线交BC于E，M，N为垂足，若BD=3，DE=4，EC=5，求证：∠B=45°．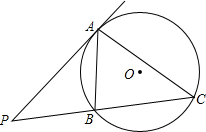
如图，P是⊙O外一点，过P作PA切⊙O于A，PC为⊙O的割线，交⊙O于点B，求证：AB2：AC2=PB：PC．
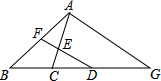如图，已知△ABG∽△FBD，△CDE∽△CGA，F是AB的中点，说明：