题目内容
 如图,已知双曲线y=
如图,已知双曲线y=| k |
| x |
| A、2 | ||
B、
| ||
| C、1 | ||
| D、4 |
考点:反比例函数系数k的几何意义
专题:计算题
分析:设B点坐标为(a,b),由矩形OABC的边AB的中点为F,则F点的坐标为(a,
),根据反比例函数y=
(k≠0)系数k的几何意义得到S△OAF=S△OEC=
|k|=
a•
,则ab=2k,软件利用S矩形=S四边形OEBF+S△OAF+S△OEC得到ab=2+
k+
k,所以2k=k+2,再解一次方程即可.
| b |
| 2 |
| k |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设B点坐标为(a,b),
∵矩形OABC的边AB的中点为F,
∴F点的坐标为(a,
),
∴S△OAF=S△OEC=
|k|=
a•
,
∴ab=2k,
∵S矩形=S四边形OEBF+S△OAF+S△OEC,
∴ab=2+
k+
k,
∴2k=k+2,
∴k=2.
故选A.
∵矩形OABC的边AB的中点为F,
∴F点的坐标为(a,
| b |
| 2 |
∴S△OAF=S△OEC=
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| 2 |
∴ab=2k,
∵S矩形=S四边形OEBF+S△OAF+S△OEC,
∴ab=2+
| 1 |
| 2 |
| 1 |
| 2 |
∴2k=k+2,
∴k=2.
故选A.
点评:本题考查了反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
| k |
| x |

练习册系列答案
相关题目
若x2+6x+m2是一个完全平方式,则实数m的值是( )
| A、3 | B、-3 |
| C、±3 | D、以上都不对 |
抛物线y=-3x2+2x-1与坐标轴的交点个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |
能够判别一个四边形是平行四边形的条件是( )
| A、一组对角相等 |
| B、两条对角线互相垂直且相等 |
| C、两组对边分别相等 |
| D、一组对边平行 |
若a+
=
,a-
的值为( )
| 1 |
| a |
| 11 |
| 1 |
| a |
A、
| ||
B、-
| ||
C、±
| ||
| D、7 |
 如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且BE=AC.求证:∠DEC=45°.
如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且BE=AC.求证:∠DEC=45°.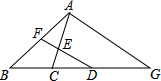 如图,已知△ABG∽△FBD,△CDE∽△CGA,F是AB的中点,说明:
如图,已知△ABG∽△FBD,△CDE∽△CGA,F是AB的中点,说明: