题目内容
20. 如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过C作CD⊥BE于D,DM⊥AB交BA的延长线于M,连接DA,
如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过C作CD⊥BE于D,DM⊥AB交BA的延长线于M,连接DA,(1)求$\frac{AB+BC}{BM}$的值;
(2)求$\frac{BC-BA}{AM}$的值.
分析 (1)延长CD交BA的延长线于点F,证△BDF≌△BDC得BC=BF、CD=FD,由DM⊥AB知DM∥AC,进而知AM=$\frac{1}{2}$AF,设AB=x,分别表示出BC、AM的长,代入计算即可;
(2)根据(1)中AB、BC、AM的长代入计算即可.
解答 解:如图,延长CD交BA的延长线于点F,
(1)∵AB=AC,∠BAC=90°,BE平分∠ABC,
∴∠FBD=∠CBD,
∵CD⊥BE,
∴∠BDF=∠BDC=90°,
在△BDF和△BDC中,
$\left\{\begin{array}{l}{∠FBD=∠CBD}\\{BD=BD}\\{∠BDF=∠BDC}\end{array}\right.$,
∴△BDF≌△BDC(ASA),
∴BF=BC,DF=DC,
设AB=x,
∴BC=BF=$\sqrt{2}$x,AF=BF-BA=($\sqrt{2}$-1)x,
又∵∠BAC=90°,DM⊥AB,
∴DM∥AC,
∵DF=DC,
∴AM=$\frac{1}{2}$AF=$\frac{\sqrt{2}-1}{2}x$
故$\frac{AB+BC}{BM}$=$\frac{AB+BC}{AB+AM}$=$\frac{x+\sqrt{2}x}{x+\frac{\sqrt{2}-1}{2}x}$=2;
(2)由(1)知AB=x,BC=$\sqrt{2}x$,AM=$\frac{\sqrt{2}-1}{2}x$,
故$\frac{BC-BA}{AM}$=$\frac{\sqrt{2}x-x}{\frac{\sqrt{2}-1}{2}x}$=2.
点评 本题主要考查全等三角形的性质与判定及三角形的中位线定理,构建全等三角形并表示出各线段的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,等边△ABC,D、E分别在AB、AC边上,且AD=CE,G为DE中点,FG⊥DE交BC于F,求证:CF=AE.
如图,等边△ABC,D、E分别在AB、AC边上,且AD=CE,G为DE中点,FG⊥DE交BC于F,求证:CF=AE.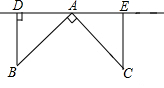 如图,点A、D、E在直线l上,∠BAC=90°,AB=AC,BD⊥l于D,CE⊥l于E,求证:DE=BD+CE.
如图,点A、D、E在直线l上,∠BAC=90°,AB=AC,BD⊥l于D,CE⊥l于E,求证:DE=BD+CE.