题目内容
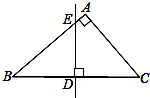 如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.
如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.考点:相似三角形的判定与性质,勾股定理
专题:
分析:首先利用勾股定理求得BC的长,然后证明△ABC∽△DBE,根据相似三角形的对应边的比相等即可求解.
解答:解:在直角△ABC中,BC=
=
=10,
则BD=
BC=5.
∵∠B=∠B,∠BDE=∠A,
∴△ABC∽△DBE,
∴
=
,即
=
,
解得:DE=
.
| AC2+AB2 |
| 62+82 |
则BD=
| 1 |
| 2 |
∵∠B=∠B,∠BDE=∠A,
∴△ABC∽△DBE,
∴
| AC |
| AB |
| DE |
| BD |
| 6 |
| 8 |
| DE |
| 5 |
解得:DE=
| 15 |
| 4 |
点评:本题考查了勾股定理和相似三角形相似的判定与性质,证明△ABC∽△DBE是关键.

练习册系列答案
相关题目
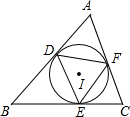 已知⊙I是锐角△ABC的内切圆,点D、E、F是三个切点,则△DEF的形状是( )
已知⊙I是锐角△ABC的内切圆,点D、E、F是三个切点,则△DEF的形状是( )| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、无法确定 |
 已知二次函数y=-x2+4x-2.
已知二次函数y=-x2+4x-2.
 如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,若S△ABC=12,则四边形BDFE的面积为
如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,若S△ABC=12,则四边形BDFE的面积为 如图,用三角尺画出△ABC关于直线MN的轴对称图形.(不写作法,保留作图痕迹)
如图,用三角尺画出△ABC关于直线MN的轴对称图形.(不写作法,保留作图痕迹)