题目内容
 如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,若S△ABC=12,则四边形BDFE的面积为
如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,若S△ABC=12,则四边形BDFE的面积为考点:三角形的面积
专题:
分析:作DM∥AE,交BC于M,根据平行线分线段成比例定理求得三角形ADF的面积,进而根据已知条件求得三角形ABE的面积,根据S四边形BDFE=S△ABE-S△ADF即可求得.
解答: 解:作DM∥AE,交BC于M,
解:作DM∥AE,交BC于M,
∴
=
,
∵AD=2BD,
∴
=
,
∴EM=
BE,
∴BE=CE,
∴
=
,
∵DM∥AE,
∴
=
=
,
∴
=
,
∴
=
,
∵AD=2BD,
∴S△ADC=
S△ABC=
×12=8,
∴S△ADF=
×8=
,
∵S△ABE=S△ACE=
S△ABC=6,
∴S四边形BDFE=S△ABE-S△ADF=6-
=
.
 解:作DM∥AE,交BC于M,
解:作DM∥AE,交BC于M,∴
| AD |
| BD |
| EM |
| BM |
∵AD=2BD,
∴
| EM |
| BM |
| 2 |
| 1 |
∴EM=
| 2 |
| 3 |
∴BE=CE,
∴
| EC |
| EM |
| 3 |
| 2 |
∵DM∥AE,
∴
| CF |
| DF |
| EC |
| EM |
| 3 |
| 2 |
∴
| CF |
| CD |
| 3 |
| 5 |
∴
| S△ADF |
| S△ADC |
| 3 |
| 5 |
∵AD=2BD,
∴S△ADC=
| 2 |
| 3 |
| 2 |
| 3 |
∴S△ADF=
| 3 |
| 5 |
| 24 |
| 5 |
∵S△ABE=S△ACE=
| 1 |
| 2 |
∴S四边形BDFE=S△ABE-S△ADF=6-
| 24 |
| 5 |
| 6 |
| 5 |
点评:本题考查三角形的面积,关键知道当高相等时,面积等于底边的比,底相等时,面积等于高的比,根据此可求出三角形的面积,然后求出差.

练习册系列答案
相关题目
(-x-y)2等于( )
| A、-x2-2xy+y2 |
| B、x2-2xy+y2 |
| C、x2+2xy+y |
| D、x2-2xy-y2 |
 如图,△ABC是⊙O的内接三角形,AB=4
如图,△ABC是⊙O的内接三角形,AB=4| 3 |
A、2
| ||
| B、4 | ||
C、2
| ||
D、4
|
 阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=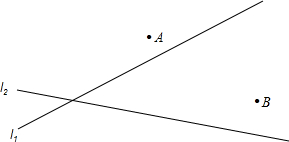 有公路l2同侧、l1异侧的两个城镇A、B,如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)
有公路l2同侧、l1异侧的两个城镇A、B,如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)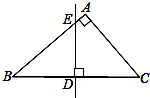 如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.
如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.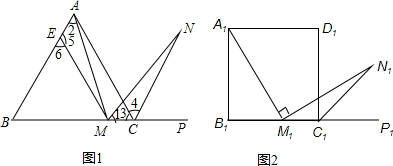
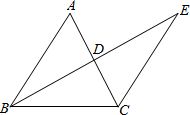 如图,BE⊥AC,垂足为D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=
如图,BE⊥AC,垂足为D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=