题目内容
证明:[请写出规范、完整的证明格式]

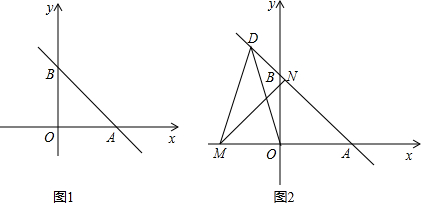
①如图1,点C是AB的中点,AD=CE,CD=BE.求证:AD∥CE.
②如图2,已知AB=AD,AC=AE,∠1=∠2,求证:△ABC≌△ADE.
③已知:如图3,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE.
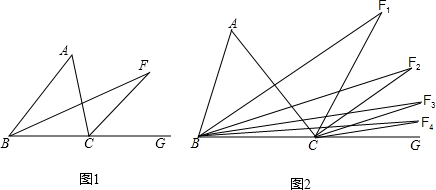
④如图4,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF求证:△ABC≌△DEF.

①如图1,点C是AB的中点,AD=CE,CD=BE.求证:AD∥CE.
②如图2,已知AB=AD,AC=AE,∠1=∠2,求证:△ABC≌△ADE.
③已知:如图3,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE.
④如图4,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF求证:△ABC≌△DEF.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)根据SSS方法可证△ACD≌△CBE,即可解题;
(2)根据SAS方法求证三角形全等即可解题;
(3)根据AAS方法求证三角形全等即可解题;
(4)根据SAS方法求证三角形全等即可解题;
(2)根据SAS方法求证三角形全等即可解题;
(3)根据AAS方法求证三角形全等即可解题;
(4)根据SAS方法求证三角形全等即可解题;
解答:证明:(1)∵C是AB的中点,
∴AC=BC,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SSS),
∴∠ACD=∠CBE,
∴AD∥CE.;
(2)∵∠1=∠2,
∴∠DAE=∠BAC,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS);
(3)∵AC∥DE,
∴∠ACD=∠D,∠BCA=∠BED,
∵∠ACD=∠B,
∴∠B=∠D.
在△ABC和△CDE中,
,
∴△ABC≌△CDE(SAS);
(4)∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
∴AC=BC,
在△ACD和△CBE中,
|
∴△ACD≌△CBE(SSS),
∴∠ACD=∠CBE,
∴AD∥CE.;
(2)∵∠1=∠2,
∴∠DAE=∠BAC,
在△ABC和△ADE中,
|
∴△ABC≌△ADE(SAS);
(3)∵AC∥DE,
∴∠ACD=∠D,∠BCA=∠BED,
∵∠ACD=∠B,
∴∠B=∠D.
在△ABC和△CDE中,
|
∴△ABC≌△CDE(SAS);
(4)∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SAS);
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中熟练运用各种方法求证三角形全等是解题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
(-x-y)2等于( )
| A、-x2-2xy+y2 |
| B、x2-2xy+y2 |
| C、x2+2xy+y |
| D、x2-2xy-y2 |
 如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O半径长为3cm,AC=10cm,则AD长度为
如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O半径长为3cm,AC=10cm,则AD长度为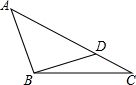 如图,已知:△ABC中,BC=6.
如图,已知:△ABC中,BC=6.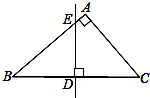 如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.
如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.