题目内容
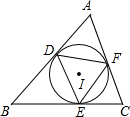 已知⊙I是锐角△ABC的内切圆,点D、E、F是三个切点,则△DEF的形状是( )
已知⊙I是锐角△ABC的内切圆,点D、E、F是三个切点,则△DEF的形状是( )| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、无法确定 |
考点:三角形的内切圆与内心
专题:计算题
分析:连接ID、IE、IF,如图,根据切线的性质得∠ADI=∠AFI=90°,则根据四边形的内角和得到∠DIF=180°-∠A,再根据圆周角定理得∠DEF=
∠DIF,
所以∠DEF=
(180°-∠A)=90°-
∠A,同理可得∠EDF=90°-
∠C,∠DFE=90°-
∠B,于是可判断△DEF为锐角三角形.
| 1 |
| 2 |
所以∠DEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:连接ID、IE、IF,如图,
∵⊙I是锐角△ABC的内切圆,点D、E、F是三个切点,
∴ID⊥AB,IF⊥AC,
∴∠ADI=∠AFI=90°,
∴∠A+∠DIF=180°,
∴∠DIF=180°-∠A,
∵∠DEF=
∠DIF,
∴∠DEF=
(180°-∠A)=90°-
∠A,
同理可得∠EDF=90°-
∠C,∠DFE=90°-
∠B,
∴∠DEF、∠DFE和∠EDF都是锐角,
∴△DEF为锐角三角形.
故选C.

∵⊙I是锐角△ABC的内切圆,点D、E、F是三个切点,
∴ID⊥AB,IF⊥AC,
∴∠ADI=∠AFI=90°,
∴∠A+∠DIF=180°,
∴∠DIF=180°-∠A,
∵∠DEF=
| 1 |
| 2 |
∴∠DEF=
| 1 |
| 2 |
| 1 |
| 2 |
同理可得∠EDF=90°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DEF、∠DFE和∠EDF都是锐角,
∴△DEF为锐角三角形.
故选C.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了圆周角定理.

练习册系列答案
相关题目
若函数y=axa2-2a-6是二次函数且图象开口向上,则a=( )
| A、-2 | B、4 |
| C、4或-2 | D、4或3 |
(-x-y)2等于( )
| A、-x2-2xy+y2 |
| B、x2-2xy+y2 |
| C、x2+2xy+y |
| D、x2-2xy-y2 |
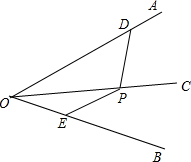 如图,OC平分∠AOB,点D,E分别在OA,OB上,点P在OC上且有PD=PE.求证:∠PDO=∠PEB.
如图,OC平分∠AOB,点D,E分别在OA,OB上,点P在OC上且有PD=PE.求证:∠PDO=∠PEB. 如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O半径长为3cm,AC=10cm,则AD长度为
如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O半径长为3cm,AC=10cm,则AD长度为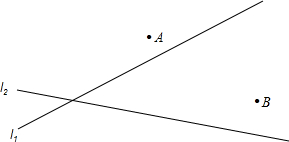 有公路l2同侧、l1异侧的两个城镇A、B,如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)
有公路l2同侧、l1异侧的两个城镇A、B,如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)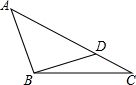 如图,已知:△ABC中,BC=6.
如图,已知:△ABC中,BC=6.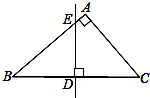 如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.
如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.