题目内容
已知在菱形ABCD中,∠D=120°,AB=8m,M从A开始以每秒一个单位的速度向B运动,N从C出发沿C→D到A方向,以每秒2个单位速度向A运动,过N作NQ⊥DC,交AC于Q.
(1)当t=2时,求NQ的长;
(2)设△AMQ面积为S,写出函数关系式及t的取值范围.
(1)当t=2时,求NQ的长;
(2)设△AMQ面积为S,写出函数关系式及t的取值范围.
考点:菱形的性质
专题:动点型
分析:(1)作AE⊥CD,交CD的延长线于E,根据菱形的性质,结合解直角三角形得出ED=
AD=4,AE=
AD=4
,CE=12,然后根据平行线分线段成比例定理即可求得NQ.
(2)分两种情况讨论求得.
| 1 |
| 2 |
| ||
| 2 |
| 3 |
(2)分两种情况讨论求得.
解答: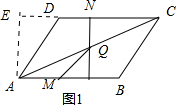 解:(1)如图1,作AE⊥CD,交CD的延长线于E,
解:(1)如图1,作AE⊥CD,交CD的延长线于E,
∵在菱形ABCD中,∠D=120°,AB=8m,
∴∠ADE=60°,
∴ED=
AD=4,AE=
AD=4
,
∴CE=8+4=12,
∵CN=2×2=4,
∵AE⊥CD,NQ⊥DC,
∴AE∥NQ,
∴
=
,
∴NQ=
×4
=
m;
(2)当0<t≤4时,如图1,
∵
=
,
∴
=
,
∴NQ=
t,
∴S△AMQ=
×AM×(AE-NQ)=
×t×(4
-
t)=-
t2+2
t,
即S△AMQ=-
t2+2
t,(0<t≤4);
当4<t≤8时,如图2,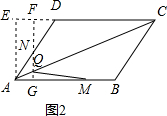 作AE⊥CD,交CD的延长线于E,
作AE⊥CD,交CD的延长线于E,
∵在菱形ABCD中,∠D=120°,AB=8m,
∴∠ADE=60°,
∴ED=
AD=4,AE=
AD=4
,
∴CE=8+4=12,
∵NQ⊥DC,
∴FD=
ND=
(2t-8)=t-4,
∴CF=t-4+8=t+4,
∵AE⊥CD,NQ⊥DC,
∴AE∥NQ,
∴
=
,即
=
,
解得,FQ=
(t+4),
∴QG=AE-FQ=4
-
(t+4),
∴S△AMQ=
×AM×QG=
×t×[4
-
(t+4)]=-
t2+2(
-1)t,
即S△AMQ=-
t2+2(
-1)t,(4<t≤8)
 解:(1)如图1,作AE⊥CD,交CD的延长线于E,
解:(1)如图1,作AE⊥CD,交CD的延长线于E,∵在菱形ABCD中,∠D=120°,AB=8m,
∴∠ADE=60°,
∴ED=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴CE=8+4=12,
∵CN=2×2=4,
∵AE⊥CD,NQ⊥DC,
∴AE∥NQ,
∴
| NQ |
| AE |
| CN |
| CE |
∴NQ=
| 4 |
| 12 |
| 3 |
4
| ||
| 3 |
(2)当0<t≤4时,如图1,
∵
| NQ |
| AE |
| CN |
| CE |
∴
| NQ | ||
4
|
| 2t |
| 12 |
∴NQ=
2
| ||
| 3 |
∴S△AMQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
| ||
| 3 |
| 3 |
即S△AMQ=-
| ||
| 3 |
| 3 |
当4<t≤8时,如图2,
 作AE⊥CD,交CD的延长线于E,
作AE⊥CD,交CD的延长线于E,∵在菱形ABCD中,∠D=120°,AB=8m,
∴∠ADE=60°,
∴ED=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴CE=8+4=12,
∵NQ⊥DC,
∴FD=
| 1 |
| 2 |
| 1 |
| 2 |
∴CF=t-4+8=t+4,
∵AE⊥CD,NQ⊥DC,
∴AE∥NQ,
∴
| FQ |
| AE |
| CF |
| CE |
| FQ | ||
4
|
| t+4 |
| 12 |
解得,FQ=
| ||
| 3 |
∴QG=AE-FQ=4
| 3 |
| ||
| 3 |
∴S△AMQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
| ||
| 6 |
| 3 |
即S△AMQ=-
| ||
| 6 |
| 3 |
点评:本题考查了菱形的性质,解直角三角形的应用,平行线分线段成比例定理的应用,三角形的面积的计算等,熟练掌握性质和定理是解题的关键.

练习册系列答案
相关题目
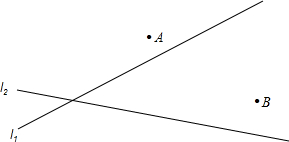 有公路l2同侧、l1异侧的两个城镇A、B,如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)
有公路l2同侧、l1异侧的两个城镇A、B,如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)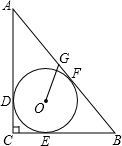 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为△ABC内切圆,与三边分别相切于D、E、F.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为△ABC内切圆,与三边分别相切于D、E、F.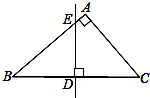 如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.
如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.