题目内容

已知二次函数y=-x2+4x-2．
（1）把它化成顶点式为
 
；
（2）在给出的坐标系中画出函数的图象．
考点：二次函数的三种形式,二次函数的图象
专题：
分析：（1）利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式．
（2）利用描点法画二次函数图象．
解答：解：（1）把它化成顶点式为y=-x2+4x-2=-（x-2）2+2，即y=-（x-2）2+2．
故答案是：y=-（x-2）2+2；
（2）由y=-（x-2）2+2知，该抛物线的顶点坐标是（2，2），抛物线的开口方向向下．
由y=-x2+4x-2知抛物线与y轴的交点坐标是（0，2）．
当y=0时，-x2+4x-2=0，
解得 x1=2+
2
，x2=2-
2

则该抛物线与x轴的交点坐标是（2+
2
，0），（2-
2
，0）．
故该抛物线的图象如图所示：
．
点评：本题考查的是二次函数的图象，熟知利用描点发画函数的图象是解答此题的关键．
练习册系列答案
相关题目
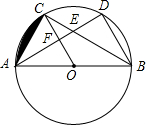如图，△ABC和△ABD都是⊙O的内接三角形，圆心O在边AB上，边AD分别与BC，OC交于E，F两点，点C为弧AD的中点；
（1）求证：OF∥BD；
（2）若点F为OC的中点，且⊙O的半径R=6cm．求阴影部分（弓形）面积．
若a，b互为相反数，则|a-2014+b|=
 
．
若函数y=axa2-2a-6是二次函数且图象开口向上，则a=（　　）
A、-2B、4
C、4或-2D、4或3
已知2006x+2007y-2007=0，若x、y互为相反数，则x=
 
，y=
 
．
计算：4sin45°-
8
+（π-
3
）0+（-1）-1=
 
．
阅读以下材料：对于三个数a，b，c，用M{a，b，c}表示这三个数的平均数，用min{a，b，c}表示这三个数中最小的数．例如：M{-1，2，3}=
-1+2+3
3
=
4
3
；min{-1，2，3}=-1；min{-1，2a}=
a(a≤-1)
-1(a＞-1)
解决下列问题：
（1）填空：min{
2
，
32
，（
2
）0}=
 
；
如果min{2，2x+2，4-2x}=2，则x的取值范围为
 
≤x≤
 
．
（2）①如果M{2，x+1，2x}=min{2，x+1，2x}=min{2，x+1，2x}，求x；
②根据①，你发现了结论“如果M{a，b，c}=min{a，b，c}，那么
 
（填a，b，c的大小关系）”
③运用②的结论，填空：若M{2x+y+2，x+2y，2x-y}=min{2x+y+2，x+2y，2x-y}
，则x+y=
 
．
（3）在同一直角坐标系中作出函数y=x+1，y=（x-1）2，y=2-x的图象（不需列表描点）．通过观察图象，
填空：min{x+1，（x-1）2，2-x}的最大值为
 
．
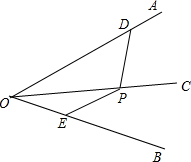如图，OC平分∠AOB，点D，E分别在OA，OB上，点P在OC上且有PD=PE．求证：∠PDO=∠PEB．
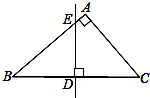如图，在△ABC中，∠A=90°，AC=6，AB=8，BC的垂直平分线交BC于D、交AB于E，求DE的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网