题目内容
已知一个口袋中装有5个只有颜色不同的球,其中3个白球,2个黑球.
(1)求从中随机抽取出两个球均是黑球的概率是多少?(用树状图或列表法求解)
(2)若往口袋中再放入x个白球和y个黑球,从口袋中随机抽出一个白球的概率是
,求y与x之间的函数关系式.
(1)求从中随机抽取出两个球均是黑球的概率是多少?(用树状图或列表法求解)
(2)若往口袋中再放入x个白球和y个黑球,从口袋中随机抽出一个白球的概率是
| 1 |
| 4 |
考点:列表法与树状图法,函数关系式
专题:
分析:(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与从中随机抽取出两个球均是黑球的情况,再利用概率公式即可求得答案;
(2)根据题意,直接利用概率公式求解可得:
=
,继而求得答案.
(2)根据题意,直接利用概率公式求解可得:
| 3+x |
| 5+x+y |
| 1 |
| 4 |
解答:解:(1)画树状图得:
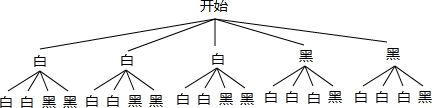
∵共有20种等可能的结果,从中随机抽取出两个球均是黑球的有2种情况,
∴从中随机抽取出两个球均是黑球的概率是:
=
;
(2)根据题意得:
=
,
∴4(3+x)=5+x+y,
∴y与x之间的函数关系式为:y=3x+7.

∵共有20种等可能的结果,从中随机抽取出两个球均是黑球的有2种情况,
∴从中随机抽取出两个球均是黑球的概率是:
| 2 |
| 20 |
| 1 |
| 10 |
(2)根据题意得:
| 3+x |
| 5+x+y |
| 1 |
| 4 |
∴4(3+x)=5+x+y,
∴y与x之间的函数关系式为:y=3x+7.
点评:此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
 如图,△ABC是⊙O的内接三角形,AB=4
如图,△ABC是⊙O的内接三角形,AB=4| 3 |
A、2
| ||
| B、4 | ||
C、2
| ||
D、4
|
 阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=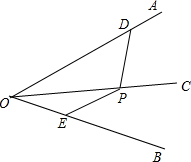 如图,OC平分∠AOB,点D,E分别在OA,OB上,点P在OC上且有PD=PE.求证:∠PDO=∠PEB.
如图,OC平分∠AOB,点D,E分别在OA,OB上,点P在OC上且有PD=PE.求证:∠PDO=∠PEB. 如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O半径长为3cm,AC=10cm,则AD长度为
如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O半径长为3cm,AC=10cm,则AD长度为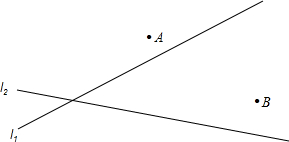 有公路l2同侧、l1异侧的两个城镇A、B,如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)
有公路l2同侧、l1异侧的两个城镇A、B,如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)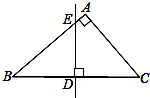 如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.
如图,在△ABC中,∠A=90°,AC=6,AB=8,BC的垂直平分线交BC于D、交AB于E,求DE的长.