题目内容
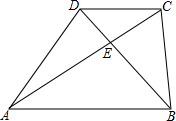四边形ABCD中，AB∥CD，AC、BD交于点E，已知S△DCE：S△ADE=4：6．（1）求
| CD |
| AB |
（2）若S△DCE=4，求四边形ABCD的面积．
考点：相似三角形的判定与性质
专题：
分析：（1）根据S△DCE：S△ADE可以求得CE：AE的值，易证△CDE∽△ABE，可得
=
，即可解题；
（2）易求得S△ADE的值，根据△CDE∽△ABE，
=
，即可求得S△ABE的值，即可解题．
| CD |
| AB |
| CE |
| AE |
（2）易求得S△ADE的值，根据△CDE∽△ABE，
| CD |
| AB |
| 2 |
| 3 |
解答：解：（1）∵△ADE和△CDE有共同的高，
∴S△DCE：S△ADE=CE：AE=4：6，
∵AB∥CD，
∴△CDE∽△ABE，
∴
=
=
，
（2）∵S△DCE：S△ADE=4：6，S△DCE=4，
∴S△ADE=6，
∵AB∥DE，
∴
=
，
∴
=
，
∴S△BCE=6，
∵△CDE∽△ABE，
=
，
∴
=
，
∴S△ABE=9，
∴四边形ABCD的面积=4+6+6+9=25．
∴S△DCE：S△ADE=CE：AE=4：6，
∵AB∥CD，
∴△CDE∽△ABE，
∴
| CD |
| AB |
| CE |
| AE |
| 2 |
| 3 |
（2）∵S△DCE：S△ADE=4：6，S△DCE=4，
∴S△ADE=6，
∵AB∥DE，
∴
| CE |
| AE |
| DE |
| BE |
∴
| S△CDE |
| S△BCE |
| 4 |
| 6 |
∴S△BCE=6，
∵△CDE∽△ABE，
| CD |
| AB |
| 2 |
| 3 |
∴
| S△CDE |
| S△ABE |
| 4 |
| 9 |
∴S△ABE=9，
∴四边形ABCD的面积=4+6+6+9=25．
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，考查了相似三角形面积比等于相似比平方的性质，本题中求证△CDE∽△ABE是解题的关键．
练习册系列答案
相关题目
如图，⊙O是正五边形ABCDE的外接圆，对角线AC、BD相交于点P．
已知平行四边形ABCD，E为AB中点，EF交AC于G点，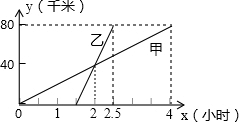
甲乙两人分别骑自行车和摩托车沿相同路线由A地到B地，图中表示他们在行驶过程中距A地的路程y（千米）和时间t（时）函数关系的图象．