题目内容
 已知⊙O1与⊙O2相交于A、B,点O1在⊙O2上,AC是⊙O1的直径,直线CB与⊙O2相交于点D,连AD.
已知⊙O1与⊙O2相交于A、B,点O1在⊙O2上,AC是⊙O1的直径,直线CB与⊙O2相交于点D,连AD.(1)求证:AD是⊙O2的直径;
(2)求证:DA=DC.
(3)若AC=2,AD=4,求sinC的值.
考点:相交两圆的性质
专题:
分析:(1)如图,作辅助线,证明∠ABD=∠ABC=90°,即可解决问题.
(2)证明DO1是线段AC的垂直平分线,即可解决问题.
(3)求出CO1=1,DC=4;借助∠CO1D=90°,运用勾股定理即可解决问题.
(2)证明DO1是线段AC的垂直平分线,即可解决问题.
(3)求出CO1=1,DC=4;借助∠CO1D=90°,运用勾股定理即可解决问题.
解答: (1)证明:如图,连接AB;
(1)证明:如图,连接AB;
∵AC是⊙O1的直径,
∴∠ABD=∠ABC=90°,
∴AD是⊙O2的直径.
(2)证明:∵AD是⊙O2的直径,
∴∠AO1D=90°,而AO1=CO1,
∴DO1是线段AC的垂直平分线,
∴DA=DC.
(3)解:∵DA=DC,DA=4,AC=2,
∴CO1=1,DC=4;而∠CO1D=90°,
∴由勾股定理得:
DO12=DC2-CO12=16-1,
∴DO1=
,
∴sinC=
.
 (1)证明:如图,连接AB;
(1)证明:如图,连接AB;∵AC是⊙O1的直径,
∴∠ABD=∠ABC=90°,
∴AD是⊙O2的直径.
(2)证明:∵AD是⊙O2的直径,
∴∠AO1D=90°,而AO1=CO1,
∴DO1是线段AC的垂直平分线,
∴DA=DC.
(3)解:∵DA=DC,DA=4,AC=2,
∴CO1=1,DC=4;而∠CO1D=90°,
∴由勾股定理得:
DO12=DC2-CO12=16-1,
∴DO1=
| 15 |
∴sinC=
| ||
| 4 |
点评:该题主要考查了相交两圆的性质及其应用问题;解题的关键是作辅助线,灵活运用圆周角定理来分析、判断、推理或解答.

练习册系列答案
相关题目
 如图,∠MON的边OM、ON上分别有点A、D,且∠MON=30°,OA=10,OD=6,B、C分别是边OM、ON上的动点,求AC+BC+BD的最小值.
如图,∠MON的边OM、ON上分别有点A、D,且∠MON=30°,OA=10,OD=6,B、C分别是边OM、ON上的动点,求AC+BC+BD的最小值. 如图,⊙O是正五边形ABCDE的外接圆,对角线AC、BD相交于点P.
如图,⊙O是正五边形ABCDE的外接圆,对角线AC、BD相交于点P. 如图:AC是⊙O的直径,弦CB平分∠ECA,BE⊥EC交⊙o于点D,连接AB、AD、BD.
如图:AC是⊙O的直径,弦CB平分∠ECA,BE⊥EC交⊙o于点D,连接AB、AD、BD.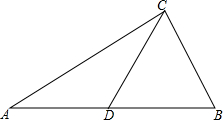 已知:如图,△ABC中,D是AB中点,若AC=12,BC=5,CD=6.5,求证:△ABC是直角三角形.
已知:如图,△ABC中,D是AB中点,若AC=12,BC=5,CD=6.5,求证:△ABC是直角三角形.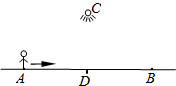 如图,夜晚,小亮从点A出发,经过路灯C的正下方点D,沿直线走到点B停止,他的影长y随他与点A之间的距离x的变化而变化.已知小亮的身高为1.6m,路灯C与地面的距离CD为4.8m,AD=BD=60m,求出y与x之间的函数表达式,并写出自变量的取值范围.
如图,夜晚,小亮从点A出发,经过路灯C的正下方点D,沿直线走到点B停止,他的影长y随他与点A之间的距离x的变化而变化.已知小亮的身高为1.6m,路灯C与地面的距离CD为4.8m,AD=BD=60m,求出y与x之间的函数表达式,并写出自变量的取值范围.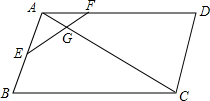 已知平行四边形ABCD,E为AB中点,EF交AC于G点,
已知平行四边形ABCD,E为AB中点,EF交AC于G点,