题目内容
 如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度.
如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度.考点:相似三角形的应用
专题:
分析:根据题意得出△ADE∽△ABC,进而利用相似三角形的判定与性质得出答案.
解答: 解:如图所示:由题意可得:AH=30m,DE=24m,BC=60m,
解:如图所示:由题意可得:AH=30m,DE=24m,BC=60m,
过点A作AF⊥BC于点F,交DE于点H,
∵DE∥BC,
∴△ADE∽△ABC,
∴
=
,
∴
=
,
解得:HF=45.
答:河宽度45m.
 解:如图所示:由题意可得:AH=30m,DE=24m,BC=60m,
解:如图所示:由题意可得:AH=30m,DE=24m,BC=60m,过点A作AF⊥BC于点F,交DE于点H,
∵DE∥BC,
∴△ADE∽△ABC,
∴
| AH |
| AF |
| DE |
| BC |
∴
| 30 |
| 30+HF |
| 24 |
| 60 |
解得:HF=45.
答:河宽度45m.
点评:此题主要考查了相似三角形的判定与性质,得出△ADE∽△ABC是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
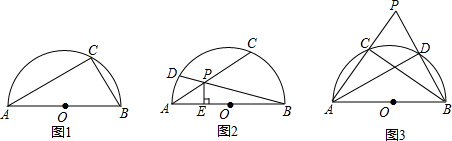
 如图,∠MON的边OM、ON上分别有点A、D,且∠MON=30°,OA=10,OD=6,B、C分别是边OM、ON上的动点,求AC+BC+BD的最小值.
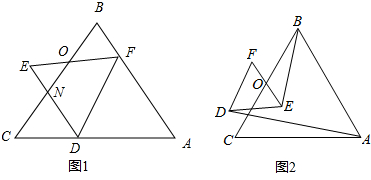
如图,∠MON的边OM、ON上分别有点A、D,且∠MON=30°,OA=10,OD=6,B、C分别是边OM、ON上的动点,求AC+BC+BD的最小值. 如图,⊙O是正五边形ABCDE的外接圆,对角线AC、BD相交于点P.
如图,⊙O是正五边形ABCDE的外接圆,对角线AC、BD相交于点P.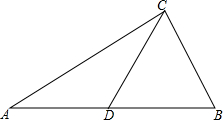 已知:如图,△ABC中,D是AB中点,若AC=12,BC=5,CD=6.5,求证:△ABC是直角三角形.
已知:如图,△ABC中,D是AB中点,若AC=12,BC=5,CD=6.5,求证:△ABC是直角三角形.