题目内容
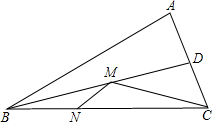 在锐角△ABC中,BC=4,∠ABC=30°,BD平分∠ABC,点M、N分别是BD、BC上的动点,连接MN、CM,则CM+MN的最小值是多少?
在锐角△ABC中,BC=4,∠ABC=30°,BD平分∠ABC,点M、N分别是BD、BC上的动点,连接MN、CM,则CM+MN的最小值是多少?考点:轴对称-最短路线问题
专题:
分析:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,则CE即为CM+MN的最小值,再根据BC=4,∠ABC=30°,由锐角三角函数的定义即可求出CE的长.
解答: 解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,
解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,
∵BD平分∠ABC,
∴M′E=M′N′,
∴M′N′+CM′=EM′+CM′=CE,
则CE即为CM+MN的最小值,
∵BC=4,∠ABC=30°,
∴CE=BC•sin30°=4×
=2.
∴CM+MN的最小值是2.
 解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,
解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,∵BD平分∠ABC,
∴M′E=M′N′,
∴M′N′+CM′=EM′+CM′=CE,
则CE即为CM+MN的最小值,
∵BC=4,∠ABC=30°,
∴CE=BC•sin30°=4×
| 1 |
| 2 |
∴CM+MN的最小值是2.
点评:本题考查的是轴对称-最短路线问题,根据题意作出辅助线,构造出直角三角形,利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
相关题目
下列各点在正比例函数y=-2x图象上的是( )
| A、(2,4) | ||
B、(6,-
| ||
| C、(-1,2) | ||
D、(
|


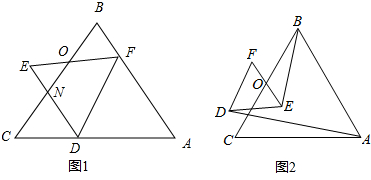
 如图,△ABC中,M为AC边的中点,E为AB上一点,且AE=
如图,△ABC中,M为AC边的中点,E为AB上一点,且AE= 如图,⊙O是正五边形ABCDE的外接圆,对角线AC、BD相交于点P.
如图,⊙O是正五边形ABCDE的外接圆,对角线AC、BD相交于点P.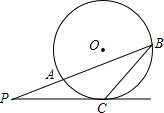 如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.
如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.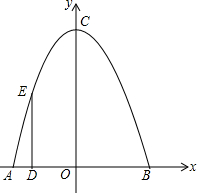 《西游记》中的孙悟空对花果山的体制进行全面改革后,为了改善旅游环境,决定对水帘洞改造翻新,计划在水帘洞前建一个由喷泉组成的水帘门洞,让游客在进入水帘洞前先经过一段由鹅卵石铺就的小道,小道两旁布满喷水管,每个喷水管喷出的水最高达4米,落在地上时距离喷水管4米.现在设如图是喷泉所经过的路线,以喷头A和喷泉落地点B的连线所在直线为横轴,AB的垂直平分线为纵轴建立平面直角坐标系.问小道的边缘距离喷水管至少应为多少米,才能使身高不高于1.75米的游客进入水帘洞时不会被水淋湿?
《西游记》中的孙悟空对花果山的体制进行全面改革后,为了改善旅游环境,决定对水帘洞改造翻新,计划在水帘洞前建一个由喷泉组成的水帘门洞,让游客在进入水帘洞前先经过一段由鹅卵石铺就的小道,小道两旁布满喷水管,每个喷水管喷出的水最高达4米,落在地上时距离喷水管4米.现在设如图是喷泉所经过的路线,以喷头A和喷泉落地点B的连线所在直线为横轴,AB的垂直平分线为纵轴建立平面直角坐标系.问小道的边缘距离喷水管至少应为多少米,才能使身高不高于1.75米的游客进入水帘洞时不会被水淋湿?