题目内容
1.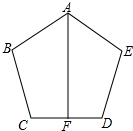 已知BC=ED,AB=AE,∠B=∠E,F是CD的中点,求证:AF⊥CD.
已知BC=ED,AB=AE,∠B=∠E,F是CD的中点,求证:AF⊥CD.
分析 连接AC、AD,由已知证明△ABC≌△AED,得到AC=AD,又因为点F是CD的中点,利用等腰三角形的三线合一可得AF⊥CD.
解答 解:如图,连接AC、AD,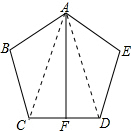
在△ABC和△AED中,
$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=ED}\end{array}\right.$,
∴△ABC≌△AED(SAS).
∴AC=AD.
∴△ACD是等腰三角形.
又∵点F是CD的中点,
∴AF⊥CD.
点评 考查了全等三角形的判定与性质;三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列方程中,是关于x的一元二次方程的是( )
| A. | 2x+1=0 | B. | 2y2+y=0 | C. | ax2+bx+c=0 | D. | x(x-2)=0 |
10.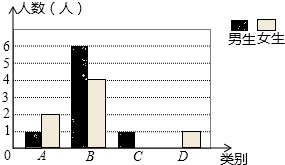 某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:
请你根据以上信息,解答下列问题:
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.
 某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:| 等级 | 分数 | 频数 | 频率 |
| A | 90≤x≤100 | 3 | 0.15 |
| B | 80≤x<90 | 10 | a |
| C | 70≤x<80 | b | 0.2 |
| D | 60≤x<70 | c | d |
| 合计 | 1 |
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.
11.下列解方程的过程,变形正确的是( )
| A. | 由$\frac{x}{3}-1=\frac{1-x}{2}$,得2x-1=3-3x | |
| B. | 由$\frac{x-2}{2}-\frac{3x-2}{4}=-1$,得2(x-2)-3x-2=-4 | |
| C. | 由$\frac{y+1}{2}=\frac{y}{3}-\frac{3y-1}{6}$-y,得3y+3=2y-3y+1-6y | |
| D. | 由$\frac{x}{4}$+1=$\frac{0.3x+1}{0.1}$+1.2,得$\frac{x}{4}$+1=$\frac{3x+10}{1}$+12 |
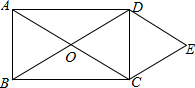 如图,在矩形ABCD中,对角线AC与BD交于点O,E是矩形ABCD外一点,且∠EDC=∠OCD,∠ECD=∠ODC,请说明CE=OA.
如图,在矩形ABCD中,对角线AC与BD交于点O,E是矩形ABCD外一点,且∠EDC=∠OCD,∠ECD=∠ODC,请说明CE=OA.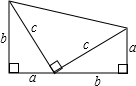 利用如图来证明勾股定理.
利用如图来证明勾股定理.