题目内容
12.已知一个正三角形和一个正六边形的面积相等,求这两个正多边形的边长的比.分析 根据题意画出图形,分别设出边长并表示出面积后即可利用面积相等得到答案.
解答 解:设正三角形的边长为a,则正六边形的边长为b;
过A作AD⊥BC于D,则∠BAD=30°,
AD=AB•cos30°=a•$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$a,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×a×$\frac{\sqrt{3}}{2}$a=$\frac{\sqrt{3}}{4}$a2;
连接OA、OB,过O作OD⊥AB;
∵∠AOB=$\frac{360°}{6}$=60°,
∴∠AOD=30°,
OD=$\frac{AD}{tan30°}$=$\frac{\frac{b}{2}}{\frac{\sqrt{3}}{3}}$=$\frac{\sqrt{3}}{2}$b,
∴S△OAB=$\frac{1}{2}$×b×$\frac{\sqrt{3}}{2}$b=$\frac{\sqrt{3}}{4}$b2,
∴S六边形=6S△OAB=6×$\frac{\sqrt{3}}{4}$b2=$\frac{3\sqrt{3}}{2}$b2,
∵S△ABC=S六边形
∴$\frac{\sqrt{3}}{4}$b2=$\frac{3\sqrt{3}}{2}$b2,
解得:a:b=$\sqrt{6}$:1.
这两个正多边形的边长的比为$\sqrt{6}$:1.
点评 本题考查了正三角形及正六边形的性质,解答此题的关键是根据题意画出图形,结合正多边形的性质解答

练习册系列答案
相关题目
2.对于非零的两个实数a、b,规定a?b=2b-a,若1?(x+1)=1,则x的值为( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | 0 |
 已知BD是等腰三角形ABC的底边AC边上的高,过点D作DE∥BC,交AB于点E
已知BD是等腰三角形ABC的底边AC边上的高,过点D作DE∥BC,交AB于点E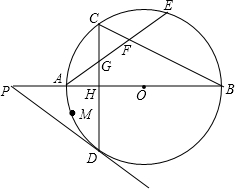 如图,AB是⊙O的直径,弦CD⊥AB于H,点E在$\widehat{BC}$上,且$\widehat{CE}=\widehat{AD}$,AE与CD交于点G,与BC交于点F.
如图,AB是⊙O的直径,弦CD⊥AB于H,点E在$\widehat{BC}$上,且$\widehat{CE}=\widehat{AD}$,AE与CD交于点G,与BC交于点F.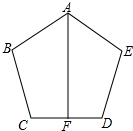 已知BC=ED,AB=AE,∠B=∠E,F是CD的中点,求证:AF⊥CD.
已知BC=ED,AB=AE,∠B=∠E,F是CD的中点,求证:AF⊥CD.