题目内容
8.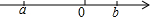 实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )
实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )| A. | -2a+b | B. | 2a-b | C. | -b | D. | b |
分析 直接利用数轴上a,b的位置,进而得出a<0,a-b<0,再利用绝对值以及二次根式的性质化简得出答案.
解答 解:由图可知:a<0,a-b<0,
则|a|+$\sqrt{(a-b)^{2}}$
=-a-(a-b)
=-2a+b.
故选:A.
点评 此题主要考查了二次根式的性质以及实数与数轴,正确得出各项符号是解题关键.

练习册系列答案
相关题目
19.不等式组$\left\{\begin{array}{l}{x+1≥2}\\{\frac{x}{2}≤1}\end{array}\right.$的解集是( )
| A. | x≤1 | B. | x≥2 | C. | 1≤x≤2 | D. | 1<x<2 |
16.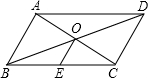 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )| A. | OE=$\frac{1}{2}$DC | B. | OA=OC | C. | ∠BOE=∠OBA | D. | ∠OBE=∠OCE |
3.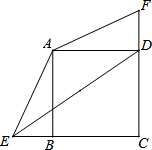 已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.
已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.
(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值.
 已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.
已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值.
13. 今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
 今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.| 评估成绩n(分) | 评定等级 | 频数 |
| 90≤n≤100 | A | 2 |
| 80≤n<90 | B | |
| 70≤n<80 | C | 15 |
| n<70 | D | 6 |
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
 已知反比例函数y=$\frac{4}{x}$.
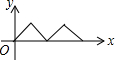
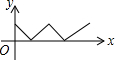
已知反比例函数y=$\frac{4}{x}$. 如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )
如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )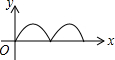
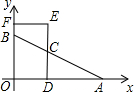 如图,在平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,2),点C为线段AB上任意一点(不与点A、B重合),CD⊥OA于点D,点E在DC的延长线上,EF⊥y轴于点F,若点C为DE的中点,则四边形ODEF的周长为( )
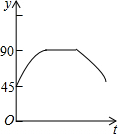
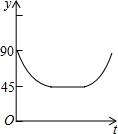
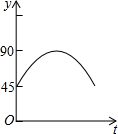
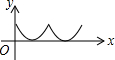
如图,在平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,2),点C为线段AB上任意一点(不与点A、B重合),CD⊥OA于点D,点E在DC的延长线上,EF⊥y轴于点F,若点C为DE的中点,则四边形ODEF的周长为( )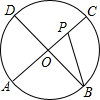 如图,AC、BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线在半径OC,劣弧$\widehat{CD}$,半径DO上作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )
如图,AC、BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线在半径OC,劣弧$\widehat{CD}$,半径DO上作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )