题目内容
13. 今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.| 评估成绩n(分) | 评定等级 | 频数 |
| 90≤n≤100 | A | 2 |
| 80≤n<90 | B | |
| 70≤n<80 | C | 15 |
| n<70 | D | 6 |
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
分析 (1)由C等级频数为15,占60%,即可求得m的值;
(2)首先求得B等级的频数,继而求得B等级所在扇形的圆心角的大小;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与其中至少有一家是A等级的情况,再利用概率公式求解即可求得答案.
解答 解:(1)∵C等级频数为15,占60%,
∴m=15÷60%=25;
(2)∵B等级频数为:25-2-15-6=2,
∴B等级所在扇形的圆心角的大小为:$\frac{2}{25}$×360°=28.8°=28°48′;
(3)评估成绩不少于80分的连锁店中,有两家等级为A,有两家等级为B,画树状图得:
∵共有12种等可能的结果,其中至少有一家是A等级的有10种情况,
∴其中至少有一家是A等级的概率为:$\frac{10}{12}$=$\frac{5}{6}$.
点评 此题考查了列表法或树状图法求概率以及扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
3.当b<0时,一次函数y=x+b的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
4.一元二次方程x2-6x-5=0配方后可变形为( )
| A. | (x-3)2=14 | B. | (x-3)2=4 | C. | (x+3)2=14 | D. | (x+3)2=4 |
8.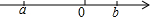 实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )
实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )
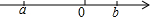 实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )
实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )| A. | -2a+b | B. | 2a-b | C. | -b | D. | b |
18.某公司的拓展部有五个员工,他们每月的工资分别是3000元,4000元,5000元,7000元和10000元,那么他们工资的中位数是( )
| A. | 4000元 | B. | 5000元 | C. | 7000元 | D. | 10000元 |
5.计算(ab2)3的结果,正确的是( )
| A. | a3b6 | B. | a3b5 | C. | ab6 | D. | ab5 |
7. 如图,正方形ABCD的周长为28 cm,则矩形MNGC的周长是( )
如图,正方形ABCD的周长为28 cm,则矩形MNGC的周长是( )
 如图,正方形ABCD的周长为28 cm,则矩形MNGC的周长是( )
如图,正方形ABCD的周长为28 cm,则矩形MNGC的周长是( )| A. | 24cm | B. | 14cm | C. | 18cm | D. | 7cm |
8. 如图,圆锥的母线长为5cm,高线长为4cm,则圆锥的底面积是( )
如图,圆锥的母线长为5cm,高线长为4cm,则圆锥的底面积是( )
 如图,圆锥的母线长为5cm,高线长为4cm,则圆锥的底面积是( )
如图,圆锥的母线长为5cm,高线长为4cm,则圆锥的底面积是( )| A. | 3πcm2 | B. | 9πcm2 | C. | 16πcm2 | D. | 25πcm2 |