题目内容
16.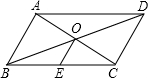 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )| A. | OE=$\frac{1}{2}$DC | B. | OA=OC | C. | ∠BOE=∠OBA | D. | ∠OBE=∠OCE |
分析 由平行四边形的性质和三角形中位线定理得出选项A、B、C正确;由OB≠OC,得出∠OBE≠∠OCE,选项D错误;即可得出结论.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB∥DC,
又∵点E是BC的中点,
∴OE是△BCD的中位线,
∴OE=$\frac{1}{2}$DC,OE∥DC,
∴OE∥AB,
∴∠BOE=∠OBA,
∴选项A、B、C正确;
∵OB≠OC,
∴∠OBE≠∠OCE,
∴选项D错误;
故选:D.
点评 此题考查了平行四边形的性质:平行四边形的对角线互相平分.还考查了三角形中位线定理:三角形的中位线平行且等于三角形第三边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.不等式3(x-1)≤5-x的非负整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.一元二次方程x2-6x-5=0配方后可变形为( )
| A. | (x-3)2=14 | B. | (x-3)2=4 | C. | (x+3)2=14 | D. | (x+3)2=4 |
11.下列数中,-3的倒数是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
8.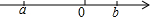 实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )
实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )
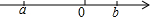 实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )
实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )| A. | -2a+b | B. | 2a-b | C. | -b | D. | b |
5.计算(ab2)3的结果,正确的是( )
| A. | a3b6 | B. | a3b5 | C. | ab6 | D. | ab5 |
11. 如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )
如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )
 如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )
如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 不变,面积为$\frac{9}{2}$ | D. | 不变,面积为4 |
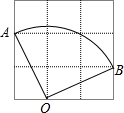 如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是$\frac{5π}{4}$.
如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是$\frac{5π}{4}$.