题目内容
3.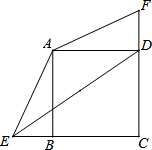 已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.
已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值.
分析 (1)根据辅助线的性质得到AD=AB,∠ADC=∠ABC=90°,由邻补角的定义得到∠ADF=∠ABE=90°,于是得到结论;
(2)过点A作AH⊥DE于点H,根据勾股定理得到AE=$\sqrt{10}$,ED=$\sqrt{C{D}^{2}+C{E}^{2}}$=5,根据三角形的面积S△AED=$\frac{1}{2}$AD×BA=$\frac{9}{2}$,S△ADE=$\frac{1}{2}$ED×AH=$\frac{9}{2}$,求得AH=1.8,由三角函数的定义即可得到结论.
解答 解:(1)正方形ABCD中,
∵AD=AB,∠ADC=∠ABC=90°,
∴∠ADF=∠ABE=90°,
在△ADF与△ABE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠ADF=∠ABE}\\{DF=BE}\end{array}\right.$,
∴△ADF≌△ABE;
(2)过点A作AH⊥DE于点H, 在Rt△ABE中,∵AB=BC=3,
在Rt△ABE中,∵AB=BC=3,
∵BE=1,
∴AE=$\sqrt{10}$,ED=$\sqrt{C{D}^{2}+C{E}^{2}}$=5,
∵S△AED=$\frac{1}{2}$AD×BA=$\frac{9}{2}$,
S△ADE=$\frac{1}{2}$ED×AH=$\frac{9}{2}$,
解出AH=1.8,
在Rt△AHE中,EH=2.6,
∴tan∠AED=$\frac{AH}{EH}=\frac{1.8}{2.6}=\frac{9}{13}$.
点评 本题考查了正方形的性质,全等三角形的判定和性质,三角形的面积倒计时,勾股定理,熟练掌握正方形的性质是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
11.下列数中,-3的倒数是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
8.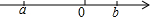 实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )
实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )
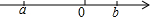 实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )
实数a,b在数轴上对应点的位置如图所示,化简|a|+$\sqrt{(a-b)^{2}}$的结果是( )| A. | -2a+b | B. | 2a-b | C. | -b | D. | b |
15.下列所述图形中,是中心对称图形的是( )
| A. | 直角三角形 | B. | 平行四边形 | C. | 正五边形 | D. | 正三角形 |
18.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |