题目内容
6. 请在括号内加注理由或在横线上填入相关内容:
请在括号内加注理由或在横线上填入相关内容:已知:如图,直线FG分别交AB、CD于点F、G,且∠1=∠2.
求证:∠A+∠AEC+∠C=360°.
证明:过点E作EH∥AB(经过直线外有且只有一条直线与已知直线平行)
∴∠A+∠3=180°(两直线平行,同旁内角互补)
∵∠1=∠2(已知)
∴AB∥CD(内错角相等,两直线平行)
∴EH∥CD(平行于同一条直线的两条直线平行)
∴∠C+∠4=180°(两直线平行,同旁内角互补)
∴∠A+∠3+∠4+∠C=180°+180°(等式性质)
即:∠A+∠AEC+∠C=360°.
分析 作出辅助线,先判断出∠A+∠3=180°,再判断出∠C+∠4=180°,即可得到结论.
解答 证明:过点E作EH∥AB(经过直线外有且只有一条直线与已知直线平行),
∴∠A+∠3=180°(两直线平行,同旁内角互补),
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
∴EH∥CD(平行于同一条直线的两条直线平行),
∴∠C+∠4=180°(两直线平行,同旁内角互补),
∴∠A+∠3+∠4+∠C=180°+180°(等式性质),
即:∠A+∠AEC+∠C=360°.
故答案为:两直线平行,同旁内角互补,内错角相等,两直线平行,EH,CD,∠3,∠4.
点评 此题是平行线的性质和判定,掌握平行线的性质和判定是解本题的关键.作出辅助线是本题的难点,是一道常规题.

练习册系列答案
相关题目
17.用分数表示4-2的结果是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
17.把方程$\frac{1}{3}$x2-x-5=0,化成(x+m)2=n的形式得( )
| A. | (x-$\frac{3}{2}$)2=$\frac{29}{4}$ | B. | (x-$\frac{3}{2}$)2=$\frac{27}{2}$ | C. | (x-$\frac{3}{2}$)2=$\frac{51}{4}$ | D. | (x-$\frac{3}{2}$)2=$\frac{69}{4}$ |
14. 如图,AB∥CD,AF平分∠BAC,且交CD于点E,若∠CEA=27°,则∠DCG的度数为 ( )
如图,AB∥CD,AF平分∠BAC,且交CD于点E,若∠CEA=27°,则∠DCG的度数为 ( )
 如图,AB∥CD,AF平分∠BAC,且交CD于点E,若∠CEA=27°,则∠DCG的度数为 ( )
如图,AB∥CD,AF平分∠BAC,且交CD于点E,若∠CEA=27°,则∠DCG的度数为 ( )| A. | 13.5° | B. | 27° | C. | 44° | D. | 54° |
16.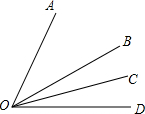 如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )
如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )
 如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )
如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )| A. | 5° | B. | 10° | C. | 15° | D. | 20° |
 如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).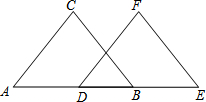 看图填空:已知,如图,BC∥EF,AD=BE,BC=EF.试说明△ABC≌△DEF
看图填空:已知,如图,BC∥EF,AD=BE,BC=EF.试说明△ABC≌△DEF 完成下面的证明(在下面的括号内填上相应的结论或推理的依据):
完成下面的证明(在下面的括号内填上相应的结论或推理的依据):