题目内容
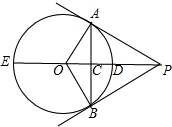 如图,PA,PB是⊙O的切线,切点分别为A,B,PO交⊙O于D、E,交AB于C,则下面的结论正确的有
如图,PA,PB是⊙O的切线,切点分别为A,B,PO交⊙O于D、E,交AB于C,则下面的结论正确的有①PA=PB;②∠APO=∠BPO;③OP⊥AB;④
 |
| AD |
 |
| BD |
考点:切线的性质
专题:
分析:先根据切线长定理得到PA=PB,∠APO=∠BPO;再根据等腰三角形的性质得OP⊥AB,∠PAB=∠PBA,AC=BC;接着根据垂径定理由OP⊥AB得
=
,然后根据切线的性质得OA⊥PA,即∠PAO=90°,根据含30度的直角三角形三边的关系,只有当∠APO=30°时,PO=2AO,由此可判断⑥不正确.
 |
| AD |
 |
| BD |
解答:解:∵PA,PB是⊙O的切线,
∴PA=PB,所以①正确;
∠APO=∠BPO,所以②正确;
∴OP⊥AB,所以③正确;
∴
=
,所以④正确;
∵PA=PB,
∴∠PAB=∠PBA,所以⑤正确;
AC=BC,所以⑦正确;
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠PAO=90°,
∴只有当∠APO=30°时,PO=2AO,所以⑥错误.
故答案为①②③④⑤⑦.
∴PA=PB,所以①正确;
∠APO=∠BPO,所以②正确;
∴OP⊥AB,所以③正确;
∴
 |
| AD |
 |
| BD |
∵PA=PB,
∴∠PAB=∠PBA,所以⑤正确;
AC=BC,所以⑦正确;
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠PAO=90°,
∴只有当∠APO=30°时,PO=2AO,所以⑥错误.
故答案为①②③④⑤⑦.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了切线长定理、垂径定理和等腰三角形的性质.

练习册系列答案
相关题目
下列各对数中,互为相反数的一对是( )
| A、-23与(-2)3 |
| B、32与-23 |
| C、2a与-2a |
| D、a与|a| |
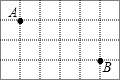 已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且△ABC为等腰三角形,则点C的个数为
已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且△ABC为等腰三角形,则点C的个数为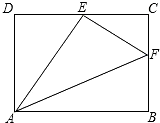 如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在边DC的中点E,折痕为AF,已知CD=8cm.求:
如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在边DC的中点E,折痕为AF,已知CD=8cm.求: 如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.
如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.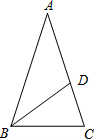 如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点.
如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点.