题目内容
 如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.
如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)怎样围才能使菜园的面积最大?最大面积是多少?
考点:二次函数的应用
专题:
分析:(1)设菜园宽为x,则长为
,由面积公式写出y与x的函数关系式,进而求出x的取值范围;
(2)利用二次函数的最值的知识可得出菜园的最大面积.
| 30-x |
| 2 |
(2)利用二次函数的最值的知识可得出菜园的最大面积.
解答:解:(1)由题意可得:
y=x(
)=-
+15x,(0<x≤18);
(2)y=-
+15x=-
(x2-30x)=-
(x-15)2+122.5,
故x=15时,y最大=112.5.
y=x(
| 30-x |
| 2 |
| x2 |
| 2 |
(2)y=-
| x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故x=15时,y最大=112.5.
点评:此题主要考查了二次函数的应用,难度一般,应注意配方法求最大值在实际中的应用.

练习册系列答案
相关题目
某种鲸鱼的体重约为1.36×105千克,关于这个近似数,下列说法正确的是( )
| A、精确到百分位 |
| B、精确到十分位 |
| C、精确到个位 |
| D、精确到千位 |
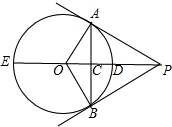 如图,PA,PB是⊙O的切线,切点分别为A,B,PO交⊙O于D、E,交AB于C,则下面的结论正确的有
如图,PA,PB是⊙O的切线,切点分别为A,B,PO交⊙O于D、E,交AB于C,则下面的结论正确的有