题目内容
16.解下列不等式组:(1)$\left\{\begin{array}{l}{2x-1≥1}\\{4-x≥0}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x-3(x-2)≤4}\\{\frac{1-2x}{4}<1-x}\end{array}\right.$.
分析 (1)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集;
(2)与(1)相同.
解答 解:(1)解不等式2x-1≥1,得:x≥1,
解不等式4-x≥0,得:x≤4,
故不等式组解集为:1≤x≤4;
(2)解不等式x-3(x-2)≤4,得:x≥1,
解不等式$\frac{1-2x}{4}$<1-x,得:x<$\frac{3}{2}$,
故不等式组的解集为:1≤x<$\frac{3}{2}$.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
6.从2,-2,1,-1四个数中任取2个不同的数求和,其和为1的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
11.下列方程组中,不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y+2=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=1}\\{xy=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=x}\\{x-2y=1}\end{array}\right.$ |
5.已知a,b,c为△ABC三边,且满足(a2-b2)(a2+b2-c2)=0,则它的形状为( )
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰三角形或直角三角形 |
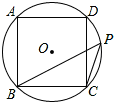 如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠BPC的度数是45°.
如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠BPC的度数是45°.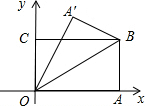 如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A′处,已知OA=$\sqrt{3}$,∠AOB=30°,则点A′的坐标是($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$),线段AA′的长度=$\sqrt{3}$.
如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A′处,已知OA=$\sqrt{3}$,∠AOB=30°,则点A′的坐标是($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$),线段AA′的长度=$\sqrt{3}$.