题目内容
6．
如图，将弧长为6π的扇形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA与OB重合（粘连部分忽略不计），则圆锥形纸帽的底面半径是3．
分析 利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，若圆锥形纸帽的底面半径为r，则2πr=6π，然后解方程即可．
解答 解：圆锥形纸帽的底面半径为r，
根据题意得2πr=6π，解得r=3，
即圆锥形纸帽的底面半径为3．
故答案为3．
点评 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，Rt△ABO的顶点O在坐标原点，点B在x轴上，∠ABO=90°，∠AOB=30°，OB=2$\sqrt{3}$，反比例函数y=$\frac{k}{x}$（x＞0）的图象经过OA的中点C，交AB于点D．
17．
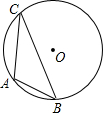如图，已知⊙O的直径为8cm，A、B、C三点在⊙O上，且∠ACB=30°，则AB长为（ ）
如图，已知⊙O的直径为8cm，A、B、C三点在⊙O上，且∠ACB=30°，则AB长为（ ）| A． | 3cm | B． | 4cm | C． | 2$\sqrt{2}$cm | D． | 2$\sqrt{3}$cm |
如图，在△ABC中，AB=AC，BD⊥AC于点D，∠A=40°，则∠CBD的度数为20°．
如图，若将左边的正方形剪成两个直角三角形和两个四边形后，恰好能拼成右边的矩形．设a=2，则正方形的边长为$\sqrt{5}$+3．
11．
如图，在四边形ABCD中，∠B=120°，∠D=50°，将∠C向内折出一个△PRC′，恰好使C′P∥AB，C′R∥AD，则∠C的度数是（ ）
如图，在四边形ABCD中，∠B=120°，∠D=50°，将∠C向内折出一个△PRC′，恰好使C′P∥AB，C′R∥AD，则∠C的度数是（ ）| A． | 80° | B． | 85° | C． | 95° | D． | 110° |
18．下列运算正确的是（ ）
| A． | $\sqrt{45}-2\sqrt{5}=\sqrt{5}$ | B． | （π-3.14）0=0 | C． | a2•a5=a10 | D． | （a+b）2=a2+b2 |
